Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.3 - Ex. 50
Seja
Esboce o gráfico de .
Se for um inteiro, calcule
Para quais valores de existe
Onde denota a função maior inteiro.
Passo 1
E aí, galerinha!
Nesse problema foi dada a função
E a partir dessa função nosso objetivo no item a) é esboçar o gráfico de .
No item b) queremos calcular
Se é um número inteiro.
E no item c) queremos saber para quais valores de o limite existe.
Tem ideia de como fazemos isso?
Primeiramente temos que entender o que é esse na função...
Essa é a função maior número inteiro, ou seja, esse termo é o maior número inteiro que assume.
Por exemplo, se , ... se , ... sacou?
Com isso em mente podemos esboçar o gráfico de por partes em intervalos de números inteiros.
Para o item b) o gráfico do item a) para determinar os limites sabendo que o limite de uma função em um ponto nada mais é que o valor que a função tende a assumir naquele ponto.
Por fim, para o item c) vamos analisar o gráfico e observar os valores de que possibilita o limite existir.
Parece muito abstrato, não é? Mas relaxa que no caminho eu te explico...
Passo 2
Vamos começar resolvendo o item a)...
Como é o maior número inteiro, vamos analisar cada intervalo inteiro de .
Por exemplo, entre , o maior número inteiro é , concorda?
Agora entre o maior número inteiro é ...
Entre o maior número inteiro é ...
Percebeu a recorrência.
Se formos escrever a função em partes, íamos obter
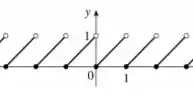
Esboçando o gráfico dessa função a partir desses intervalos, vamos chegar em
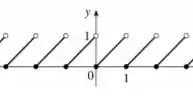
Tranquilo até aqui?
Passo 3
Agora no item b) temos que calcular os limites
Se é um número inteiro podemos reescrever nossa função para cada um dos casos
Para , vemos que se aproxima de pela esquerda.
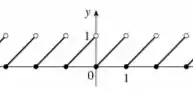
Pelo gráfico, vemos que nesses pontos tende a , então podemos dizer que .
Agora se ( tende a pela direita) pelo gráfico observamos que nos números inteiros, a função tende a .
Então podemos dizer que
Bacana, não é?
Passo 4
Por fim, vamos determinar os valores de , tais que
Exista...
O limite de uma função não vai existir em dois casos... caso a função tenda a ou e caso tenha um ponto na função onde e , ou seja, os limites laterais são diferentes...
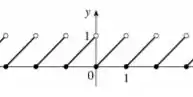
Pelo gráfico da função, vamos que não tende a ou em nenhum momento, porém, temos alguns pontos que tem descontinuidade.
Perceba que para inteiros, o gráfico tem uma descontinuidade
Portanto para que o limite exista, não pode ser um número inteiro...
E fim!! O que achou? Reponde Aí!
Resposta
