Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.4 - Ex. 64

Em 7 de maio de 1992 o ônibus espacial Endeavour foi lançado na missão STS- 49 cujo propósito era instalar uma peça nova em um satélite de comunicação do INTELSAT. A tabela dá os dados da velocidade para o ônibus entre o lançamento e a entrada em ação dos foguetes auxiliares.

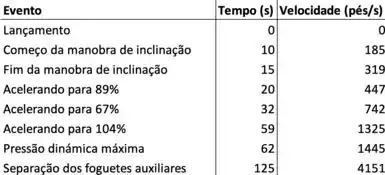
  1. Use uma calculadora gráfica ou computador para modelar esses dados por um polinômio de terceiro grau.

  2. Use o modelo da parte ( a ) para estimar a altura atingida pela Endeavour 125 segundos depois do lançamento.

Passo 1

Fala aí pessoal 😊!

Nesse exercício temos uma tabela que mostra a velocidade do ônibus espacial de acordo com o tempo desde o seu lançamento.

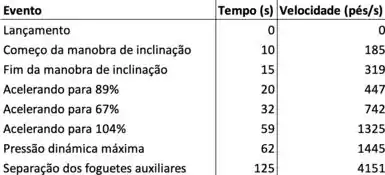
Com essas informações, precisamos fazer duas coisas:

  • No item ( a ) : Modelar os dados da tabela por um polinômio de terceiro grau, usando uma calculadora gráfica ou computador para isso.
  • No item ( b ) : Estimar a altura que o ônibus espacial atingiu após 125 segundos do seu lançamento, usando o polinômio obtido no item anterior.

🤔 Bem, mas como vamos fazer isso?

No item ( a ) precisamos de alguns conhecimentos sobre computadores ou calculadoras gráficas. O polinômio pode ser obtido usando um software como o Excel ou a biblioteca numpy do Python, por exemplo.

Já no item ( b ) , pra encontrar a altura do ônibus espacial (que nesse caso é o deslocamento), vamos ter que calcular a integral definida

∫ 0 125 v t d t ,

onde v ( t ) é a nossa estimativa para a velocidade obtida no item ( a ) , beleza?

🛠️ Sabendo disso, vamos relembrar de algumas ferramentas que vão nos ajudar a resolver esse exercício:

  • Parte 2 do Teorema Fundamental do Cálculo: se a função f é contínua no intervalo [ a ,   b ] então

    • ∫ a b f t d t = ∫ f t d t a b

    onde ∫ f t d t é a primitiva da função f , ou seja,

    d d t ∫ f ( t ) d t   = f t .

  • A integral indefinida de uma soma de funções é a soma das integrais indefinidas de cada uma das funções.

    • ∫ f t + g t d t =   ∫ f t d t +   ∫ g ( t ) d t .

  • A integral indefinida do produto entre uma constante e uma função é o produto entre a constante e a integral indefinida da função.

∫ c f t d t =   c ∫ f ( t ) d t .

  • Regra da Potência: para qualquer n ≠ 1 ,   a integral indefinida da função t n é a função

    • ∫ t n   d t = t n + 1 n + 1 + B ,

    onde B é uma constante qualquer.

    Bem, isso é tudo o que precisamos para resolver a questão! Bora lá 😊?

    Passo 2

    Item a :   Modelar os dados da tabela por um polinômio de terceiro grau, usando uma calculadora gráfica ou computador para isso.

    Vamos encontrar o polinômio de grau 3 que melhor aproxima os dados! Um jeito de fazer isso é seguir os seguintes procedimentos:

  • Escrever os valores da tabela em uma planilha do Excel.
  • Inserir um gráfico de dispersão usando os dados inseridos.
  • Clicar nos dados no gráfico e adicionar uma linha de tendência polinomial de grau 3.

Fazendo esses procedimentos, vamos obter um gráfico como esse aqui.

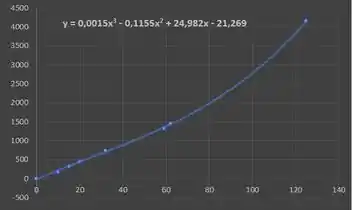
Com ele, podemos ver que

v t = 0,0015 t 3 - 0,1155 t 2 + 24,982 t - 21,269 .

Pronto, vamos agora para o item b !

Passo 2

Item b : Estimar a altura que o ônibus espacial atingiu após 125 segundos do seu lançamento, usando o polinômio obtido no item anterior.

Como vimos no Passo 1 , para isso, vamos calcular a integral

∫ 0 125 v t d t .

Como pela Parte 2 do Teorema Fundamental temos que

∫ 0 125 v ( t ) d t =   ∫ v ( t )   d t 0 125 ,

então como vale que

v t = 0,0015 t 3 - 0,1155 t 2 + 24,982 t - 21,269 ,

Vamos precisar encontrar a integral indefinida

∫ ( 0,0015 t 3 - 0,1155 t 2 + 24,982 t - 21,269 )   d t .

Para isso, usamos as propriedades das integrais indefinidas dadas no Passo 1 .

Logo,

∫ v ( t )   d t = 0,0015 4 t 4 - 0,1155 3 t 3 + 24,982 2 t 2 - 21,269 t + C .

Ou seja,

∫ v ( t )   d t = 0,000375 t 4 - 0,0385 t 3 + 12,491 t 2 - 21,269 t + C .

Passo 3

Agora, só precisamos usar a Parte 2 do Teorema Fundamental, beleza?

De fato, como

∫ 0 125 v ( t ) d t =   ∫ v ( t )   d t 0 125 ,

então precisamos obter o valor da integral indefinida ∫ v ( t )   d t nos pontos extremos do intervalo de integração.

Em t =   125

∫ v ( t )   d t ​ t = 125 = 0,000375 ⋅ 125 4 - 0,0385 ⋅ 125 3 + 12,4912 ⋅ 125 2 - 21,269 ⋅ 125 + C ,

ou seja,

∫ v ( t )   d t ​ t = 125 ≈ 208 . 870 , 67 + C .

Em t = 0

∫ v ( t )   d t ​ t = 0 = C .

Substituindo esses valores na igualdade do Teorema, temos que:

∫ 0 125 v t d t ≈ 208 . 870 , 67 + C - C .  

Dessa forma, a integral procurada vale

∫ 0 125 v t d t ≈ 208 . 870 , 67 .

Com isso, temos que a altura atingida é aproximadamente 208870 , 67 pés.

Resposta

Para o item ( a ) , encontramos

v t = 0,0015 t 3 - 0,1155 t 2 + 24,982 t - 21,269 .

Para o item ( b ) , encontramos que a altura atingida é aproximadamente 208 . 870 , 67 pés.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral.int_1^2 (1)/(x^2) - (4)/(x^3) d x
Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. g ( s ) = ∫ 5 s t - t 2 8 d t
Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função.10) g ( r ) = ∫ 0 r x �� + 4 . d x ��
Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função.8) g ( x ) = ∫ 3 x e t 2 - t . d t
Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. h ( x ) = ∫ 1 e x ln ⁡ t d t