Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.4 - Ex. 12
Para o limite
Ilustre a definição encontrando os valores de que correspondam a e .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente ilustrar a definição do limite dado, encontrando os valores de delta () que correspondam a e .
Nosso limite é dado por:
Uma das definições de limite, nos diz que se temos uma função definida em um intervalo aberto que contenha o número , exceto possivelmente no próprio , então:
significa que para todo número positivo há um número positivo correspondente tal que:
sempre que
Ilustrando isso, teríamos algo assim:
Isso diz que o valor de pode ser arbitrariamente grande (maior que qualquer número dado) tornando-se suficientemente próximo de (dentro de uma distância , onde depende de , mas com ).
Então, dada qualquer reta horizontal , podemos achar um número positivo tal que, se restringirmos a ficar no intervalo , então a curva ficará acima da reta .
No nosso caso, , está tendendo a zero, então e temos na letra (a) e na letra (b). Precisamos encontrar o valor de em ambos os casos.
Pra isso, precisamos analisar o gráfico da função cotangente de e encontrar os valores de próximos de que fazem com que a função esteja acima do valor de dado em cada caso.
Vamos lá!
Passo 2
Vamos começar plotando a função cotangente ao quadrado. Pra isso, a gente precisa ter em mente que essa função é periódica, se repetindo a cada intervalo de ao longo do eixo . Além disso, a função tem assíntotas verticais em (onde é um número inteiro) e que como ela é definida por:
Então, ela não está definida para , porque o seno de zero é zero e a gente não pode ter um denominador nulo na fração, certo?
Sabendo dessas características, nós vamos ter algo mais ou menos assim:
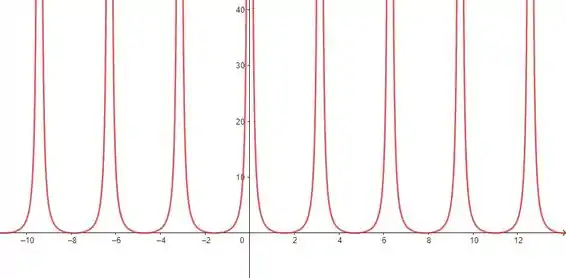
Agora se a gente der um zoom mais próximo de , no eixo horizontal, e plotarmos a reta , vamos ter algo assim:
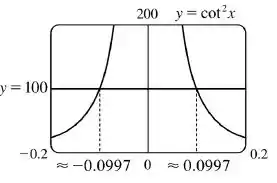
Observe que a curva encontra a reta em aproximadamente e . Isso significa que restringindo a ficar no intervalo , então a curva ficará acima da reta .
Portanto, escolhendo de modo que se então, .
Passo 3
Da mesma forma, se traçarmos a reta no gráfico da cotangente ao quadrado, visto no passo anterior, e dermos um zoom próximo a zero, vamos ter:
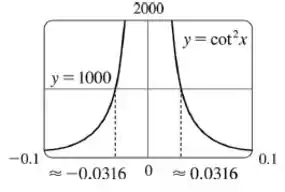
Observe que agora a curva encontra a reta em aproximadamente e . Isso significa que restringindo a ficar no intervalo , então a curva ficará acima da reta .
Portanto, escolhendo de modo que se então, .
Observe que se o escolhido for um número muito grande, então o um cada vez menor será necessário.
Valeu, galera! Até a próxima! 😉