Seja .
- Estime os valores de , e fazendo uso de uma ferramenta gráfica para fazer um zoom no gráfico de .
- Use a simetria para deduzir os valores de , , e .
- Empregue os valores de e para fazer o gráfico de .
- Conjecture uma fórmula para .
- Use a definição de derivada para demonstrar que sua conjectura em está correta.
Passo 1
Preparados para fazer esse exercício e ficar com uma base fera em derivadas? Bora ficar monstro em cálculo!
Antes de começar valendo, vale ressaltar uma coisinha: o exercício pede para usarmos uma ferramenta gráfica para realizar os procedimentos da questão e, realmente, isso vai ser necessário. Caso você não tenha uma calculadora gráfica, pode procurar usar softwares como o Geogebra ou Scilab que são gratuitos e muito bons para fazer uma imensidão de tarefas!
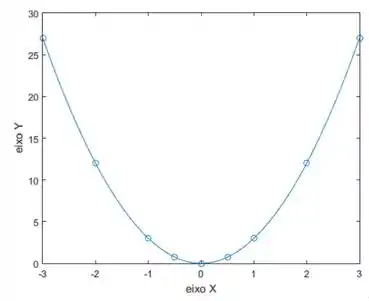
Primeiro vamos fazer o gráfico de , usando uma ferramenta gráfica.
Na letra a, queremos estimar os valores de , e , apenas dando zoom no gráfico e calculando, de forma aproximada mesmo. Ahhh.. lembra que a derivada da função num ponto é a inclinação da reta tangente naquele ponto (o coeficiente angular).
Na letra b, vamos usar a simetria da função pra deduzir os valores de , , e .
Na letra c, vamos usar o que obtivemos nas letras a e b para esboçar o gráfico de Achamos vários pontos, né? Daí é só traçar a linha ligando esses pontos.
Na letra d, vamos, a partir do gráfico da letra c, deduzir uma fórmula para
Na letra e, vamos mostrar que a fórmula que deduzimos na letra d usando a definição de derivada, que é aquele limite, lembra?
Passo 2
- A primeira coisa que vamos fazer é plotar o gráfico de , Dá uma olhada:
- Como a função é uma função ímpar, ou seja:
- Vamos pegar os valores de todas as derivadas que temos e organizar uma tabela! Vai ficar assim olha:
- Olhando pra função que a gente desenhou no item c, a gente repara que é uma parábola, certo? Então podemos supor que ela tem o formato de uma parábola:
- Agora vamos treinar umas continhas e resolver a derivada de pela definição! Caso você não esteja lembrando como ela é, dá uma olhadinha:
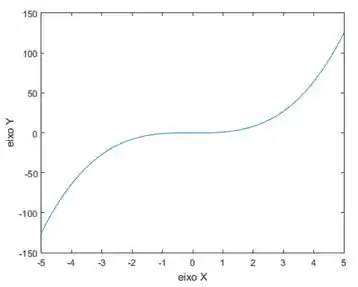
Agora, iremos dar o zoom em cada ponto do gráfico em que nós é pedido para encontrar a derivada. Se aproximarmos bem, vai chegar um momento em que vamos acabar enxergando uma reta, e essa reta é como se fosse uma aproximação da nossa reta tangente ao ponto. Olha como fica se aproximarmos perto da região em torno de :
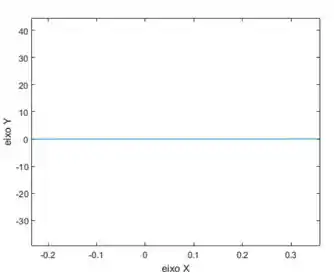
Ta tipo uma reta na horizontal né? Sabemos que uma reta na horizontal não tem inclinação e, como essa inclinação é justamente o valor da derivada no ponto, podemos estimar então que .
Passo 2
Continuando nossas estimações a partir do gráfico, dando o zoom no ponto vamos ficar com isso aqui:
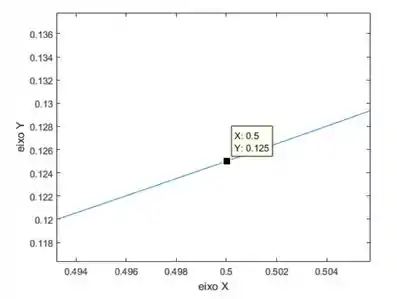
Perceba que, nessa reta, temos os pontos e . Podemos usar esses caras para calcular a inclinação dessa reta aí através da fórmula:
Vamos aplicar ela aos valores que temos:
Isso quer dizer que, pela nossa estimativa, .
Passo 3
Indo agora para o ponto :
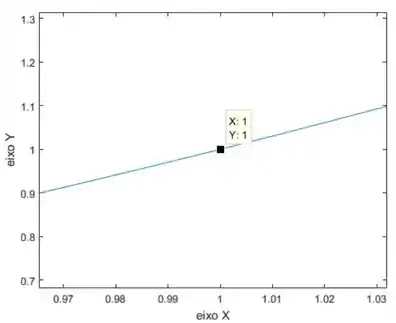
Aqui vamos utilizar os pontos e para estimar a derivada. Teremos então:
Logo, a partir dessa continha aí, estimamos que
Passo 4
Dando o zoom agora em :
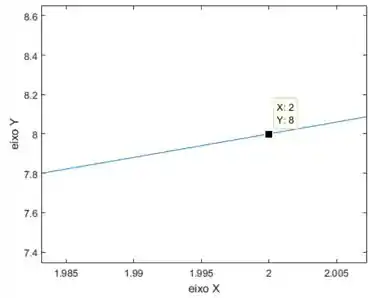
Pegando os pontos e vamos ter:
Assim, nossa nos diz que .
Passo 5
Falta só mais uma derivada para estimarmos! Trabalhando agora com :
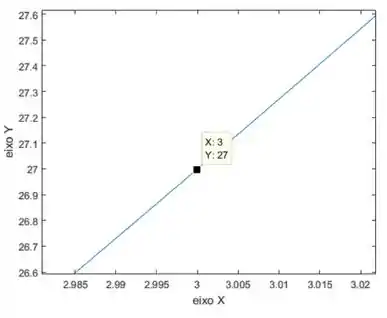
Pegando os pontos e vamos ter:
Terminamos nossa última aproximação gráfica! Aqui, estimamos que .
Passo 6
Podemos usar um propriedade da derivada que diz que, se a é ímpar, então com certeza é par, sacou? Lembrando que a função par é aquela que obedece a seguinte lei:
Assim, de forma direta, podemos dizer que , , e .
Passo 7
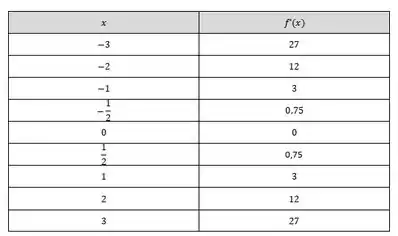
Dá para ver que é uma função par, com valores sempre positivos e que corta o eixo em . Plotando os pontos em um gráfico, teremos esse comportamento para :
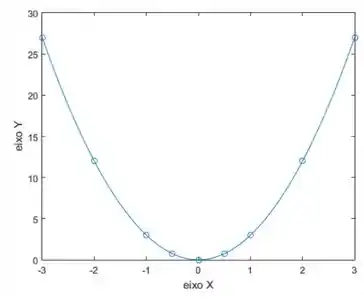
Passo 8
E temos alguns pontos pra achar os valores de , e .
Quando , :
Aí já reduzimos a parábola para:
Quando
Quando
Daí resolvemos o sistema:
E achamos:
Então a equação da parábola será:
Passo 9
Sabemos que e já vamos substituir na fórmula. Além disso, . Saca só como vai ficar:
O termo é um produto notável cubo da soma, então a gente consegue expandir ele desse jeitinho aqui:
Cancelando com :
Agora, nós vamos colocar o do numerador em evidencia, ta bom? Assim podemos cancelar com o do denominador:
Beleza, nosso limite tá prontinho para ser resolvido! Tudo o que precisamos fazer é a substituição para rencontrar nosso resultado:
Prontinho! Nosso resultado mostra que, pelo visto, a derivada é realmente , o que encerra o nosso exercício!
Resposta
- e e
- e e
- Pelos dados mostrados, o gráfico de será:
- A partir do gráfico e das derivadas encontradas, chegamos à conclusão de que a fórmula provável para é
- Utilizando a definição de derivada, foi possível demonstrar que o item está correto e que