Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.3 - Ex. 28
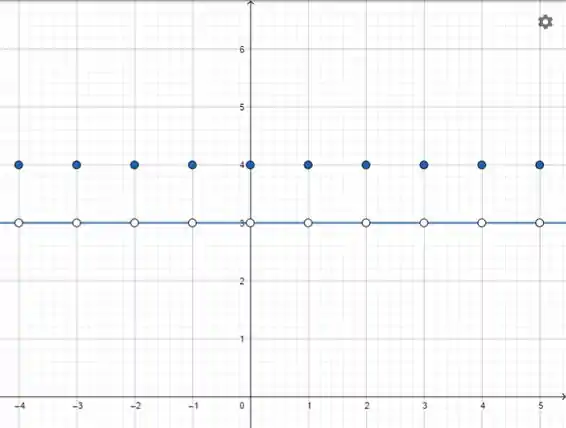
Seja . Faça um esboço do gráfico de .
Ache, se existirem
Passo 1
Vamos começar entendendo que diabos de função é aquele que ele deu.
Essa função é a chamada de “parte inteira”. Mas o que isso significa? O valor de vai ser a parte inteira do que está dentro desses colchetes duplos.
Por exemplo:
E por ai vai, entendeu?
Agora precisamos entender como vai funcionar isso com a que tem duas dessas funções.
Vamos analisar em dois casos, se for um inteiro e se não for um inteiro.
Se for inteiro, vamos ter
Porque ele não tem parte decimal.
Porque não vai ter parte decimal, então
Agora, se for decimal, vamos colocar o entre dois inteiros tá bem?
Porque fazemos isso? Porque aquele na verdade vai ser a parte inteira de , já que vai ser o mais alguns décimos e tudo mais.
Então vamos ter
Beleza, mas e o
Pegando
Multiplicando por vamos ter
Somando com , para chegarmos na expressão dentro dos colchetes duplos
Repara que tanto , quanto são interiros? A parte interira de vai ser o menor deles, que é o . Então
E a nossa fica
Então teremos
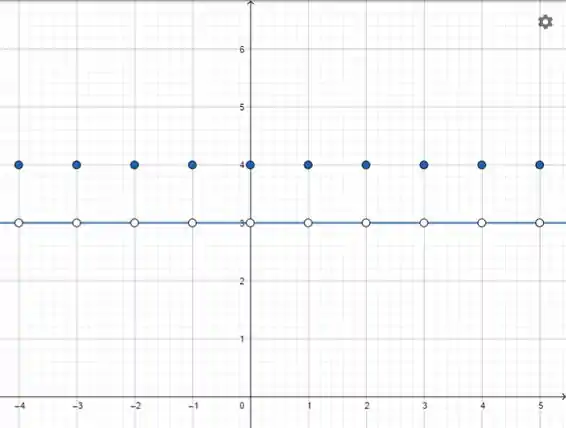
O gráfico é uma reta, em fora dos inteiros e quando for inteiro devemos ter .
Isso faz com que, na reta , tenha que se colocar bolas abertas nos inteiros e em cada inteiro se tenha bolas fechadas em .
Passo 2
Letra
Agora vamos aos limites que ele pediu
Aqui, temos que ver o comportamento da função quando se aproxima de pela direita. Que é se aproximar de por valores maiores que .
Olhando o gráfico, em valores MAIORES que , a se aproxima de . Mesmo que no a função tenha valor .
Então
Passo 3
Letra
Agora o outro
Aqui, temos que ver o comportamento da função quando se aproxima de pela esquerda. Que é se aproximar de por valores menores que .
Olhando o gráfico, em valores MENORES que , a se aproxima de . Mesmo que no a função tenha valor .
Então
Passo 4
Letra
Para o limite que ele pediu, temos que comparar os limites laterais.
Se eles forem iguais, o limite em vai existir e será esse valor. Se eles forem diferentes o limite não existe.
Pelas letras e , os dois limites laterais são e , respectivamente.
Como eles são iguais, o limite vai ser
Resposta
