Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.4 - Ex. 42
42. a) Encontre os valores de e na figura abaixo.
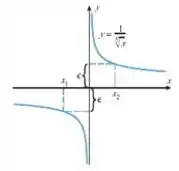
b) Encontre um número positivo , tal que:
Com .
c) Encontre um número negativo , tal que:
Com .
Passo 1
a) Então galera, aqui não possui muito segredo não, ok? O valor da função correspondente ao ponto é , logo:
E o valor da função correspondente ao ponto é , logo:
Passo 2
b) Temos a seguinte desigualdade, pessoal:
Isolando teremos:
E como , temos que:
Passo 3
c) Seguindo o mesmo raciocínio do passo anterior, temos que:
Isolando teremos:
Uma vez que , é por isso que aparece o sinal negativo, galera! Comparando os resultados:
E está aí nossa resolução, pessoal! 😊
Resposta
a)
b)
c)
Exercícios de Livros Relacionados
Para o limite lim x → - ∞ 1 - 3 x x 2 + 1 = 3 Ilustre a Definição8 encontrando os valores de N que corresponde a ε = 0,1eε = 0,05 .
Determine o limite infinito.
35. Determine o limite infinito. lim x → 5 + ln ( x 2 - 25 )
Determine o limite infinito.
Determine o limite infinito.