Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 13.Exercícios - Ex. 377
Seja a função
- Determine os valores de x tais que f(x) = 0.
- Esboce o gráfico de g.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de funções circulares inversas.
Item a
De acordo com o enunciado teremos que resolver o seguinte problema:
Sabendo que:
Comparando com o problema do item dado, temos que:
Daí teremos que:
Passo 2
Para esboçarmos o gráfico pedido, devemos encontrar alguns pontos importantes deste, detalhados na tabela abaixo (Calculados com o auxílio de uma calculadora científica):
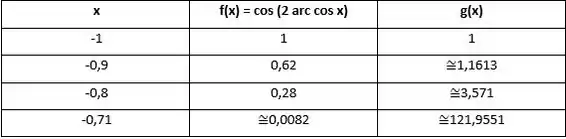
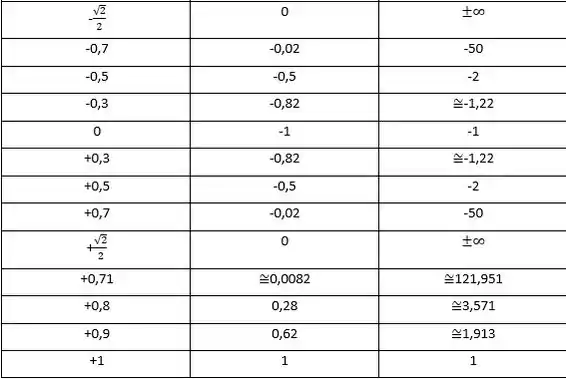
Devemos notar a simetria existente entre os intervalos , que tem g(x) indo para quando f(x) se aproxima de 0, e também a simetria entre os intervalos
, onde g(x) tende a quando f(x) se aproxima de 0.
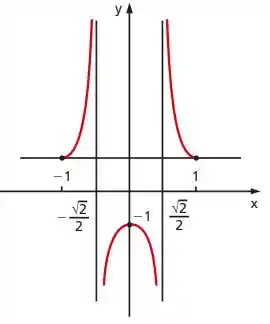
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.
Resposta
Ver passo a passo.
Exercícios de Livros Relacionados
Prove que arctan a - a r c c o t g b = a r c c o t g b - a r c c o t g a .
Se f (theta) = tan theta . Verifique a igualdade f (2 theta) = (2 f (theta))/(1 - [f (theta)]^2) .
Estude a variação da função f (x) = (1 - cos 2 x)^((1)/(2)) * (1 + cos 2 x)^(- (1)/(2))
Qual é o período da função f (x) = (1 + t g x)/(1 - t g x) ?
Estude a variação da função f: R ➞ R dada por f (x) = s e n 2 x + c o s 2 x