Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.6 - Ex. 37

Seja s = 2 t 2 + 1 a função posição de uma partícula movendo-se ao longo de um eixo coordenado.

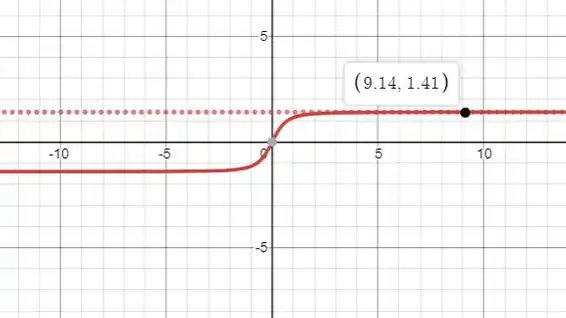
  1. Use um recurso gráfico computacional para gerar o gráfico de v versus t e faça uma conjectura sobre a velocidade da partícula quando t → + ∞ .
  2. Verifique sua conjectura obtendo lim t → + ∞ ⁡ v .

Passo 1

  1. Para achar v t vamos derivar a expressão de s t :

    2. v t = s ' t = 1 2 2 t 2 + 1 1 2 - 1 2 ⋅ 2 ⋅ t 2 - 1 + 0 = 1 2 2 t 2 + 1 - 1 2 4 t = 2 t 2 t 2 + 1

    Pronto, vamos agora gerar o gráfico de v t :

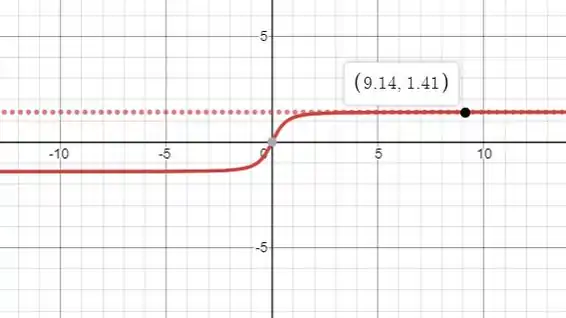
    Analisando o gráfico temos que a velocidade da partícula quando t → + ∞ é de 1,41 m/s.

    Passo 2

  2. Vamos agora fazer lim t → + ∞ ⁡ v para checar nossa resposta da letra (a):

lim t → + ∞ ⁡ 2 t 2 t 2 + 1 = lim t → + ∞ ⁡ 2 t t 2 2 + 1 t 2 = lim t → + ∞ ⁡ 2 t t 2 + 1 t 2 = lim t → + ∞ ⁡ 2 2 + 1 t 2 = 2 2 + 0 = 2 2 =

= 2 2 ⋅ 2 2 = 2 2 2 = 2 = 1,41

Pronto, achamos a mesma resposta.

Resposta

    2. v = 1,41 m/s

  2. lim t → + ∞ ⁡ 2 t 2 t 2 + 1 = 1,41
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o roteiro desta seção para esboçar a curva: y = s e n 3x
Use o roteiro desta seção para esboçar a curva: y = x 3 x - 2
Use o roteiro desta seção para esboçar a curva: y = x - 3 x
Use o roteiro desta seção para esboçar a curva: y = e x / x 2
Use o roteiro desta seção para esboçar a curva: y = ln ⁡ ( s e nx )