Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 (exercícios de compreensão) - Ex. 4
Seja:
(a) A letra do alfabeto que mais se parece com o gráfico de é ________.
(b) é uma função par?
Passo 1
(a) Vamos entender esse problema de dois jeitos: um em que não precisamos plotar o gráfico e outro que vamos apenas plotar e responder. Primeiro, vamos ver sem plotar.
Nesse capítulo, vimos translações de gráficos, que ficou muito bem resumido na tabela 0.2.2. Então, de acordo com os princípios da translação, quando somamos uma constante positiva ao , deslocamos o gráfico para a esquerda. E, quando subtraímos uma constante positiva ao , deslocamos o gráfico para a direita. Certinho?
Vamos olhar para a :
Apesar dela ser uma função por partes, vemos que temos duas funções parecidas com a função módulo , a diferença são o somado ao na primeira e subtraído na segunda condição. Logo, seria o deslocado para a esquerda e para a direita. Como tem o formato de um “V”, podemos concluir que, como a possui dois “V’s”, deve ter um formato de W (w parece a junção de dois v’s né).
Passo 2
Agora, vamos plotar para ver que isso tudo é verdade?
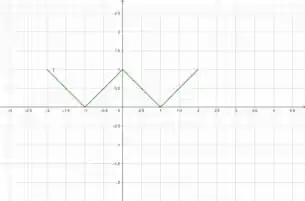
Olha só! Não falei? Hahah como a gente já esperava! Um “W”.
Passo 3
(b) Qual a definição de uma função par? Bom, uma função é par se:
Ou seja, se ela tem uma simetria em relação ao eixo , certo?
Olhando para o gráfico do passo anterior, podemos imaginar que seja par sim, pois tem um “V” antes do eixo vertical e outro “V” igualzinho depois.... Além disso, temos que a função módulo é par e nossa é uma junção de funções módulo... Mas vamos ter certeza disso!
Vamos pegar um ponto positivo e o seu oposto e vamos ver quais valores a assume nesses pontos:
Em , (entra na segunda condição), substituindo por :
Em , (entra na primeira condição), substituindo por :
Opa, como , nossa condição para a função ser par foi satisfeita!
Resposta
(a) W.
(b) Sim.