Expresse a função na forma por partes, sem usar valores absolutos. [Sugestão: Pode ser útil gerar o gráfico da função.]
(a)
(b)
Passo 1
(a) Então temos a função e queremos escrevê-la por partes, o que seria isso? Vamos procurar uma lógica de formação dessa função a partir de intervalos de . Ou seja, ela vai assumir um valor até um ponto e, a partir dele, assume outro valor. Vamos ver isso com calma.
Vamos usar a sugestão do problema e olhar para a função, para entender melhor do que se trata:
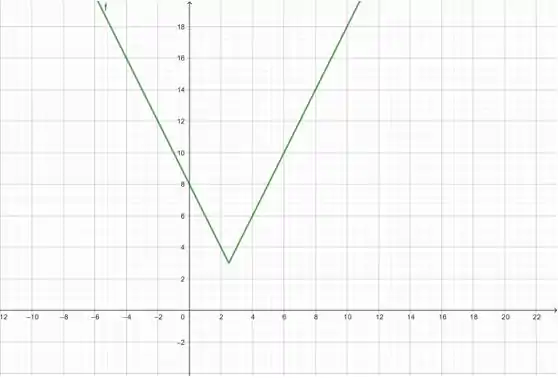
Essa é a nossa função. E você pode ver que até o ela parece ter um comportamento e, a partir dele, outro comportamento. Nosso intuito é descobrir esses comportamentos! Vamos lá!
Passo 2
Como podemos fazer isso? Cara, a função módulo tem a característica de “ignorar” o sinal, certo? Se for positivo, continua sendo, mas se for negativo, passa a ser positivo. Tudo fica positivo! Ou seja, se for positivo, continua sendo , mas se for negativo, fazemos e calculamos o valor da função.
Para achar os comportamentos de uma função assim, nós substituímos o por (pegando os valores positivos do ) e por (pegando os valores negativos do ) e vamos achar uma função diferente para cada substituição do .
Obs.: quando trocamos o sinal do módulo, trocamos o sinal de tudo que está dentro do módulo!
Então, vamos usar o , primeiro:
Essa é a função para os valores maiores que .
Para os negativos, faremos :
Essa é a função para os valores menores que .
Agora, é só juntar essas duas informações! No fim do dia, temos que:
Prontinho!
Passo 3
(b) Então temos a função e queremos escrevê-la por partes. A ideia será a mesma da letra anterior, ok? Só vai mudar a função.
Vamos usar a sugestão do problema e olhar para a função, para entender melhor do que se trata:
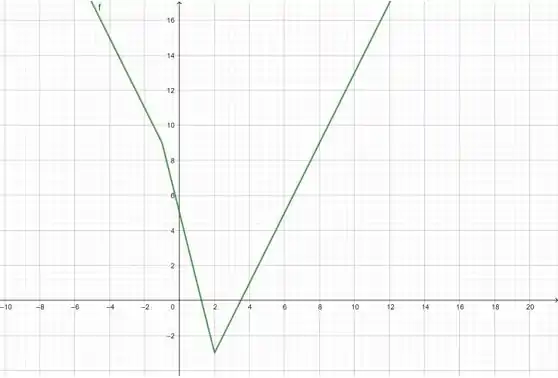
Qual vai ser a grande diferença dessa função para a da letra anterior? Repare ali que temos 3 comportamentos diferentes: um até o , outro dali até e o último a partir daí. Por quê isso?
Porque agora temos dois módulos na função. Então, agora, vamos pegar valores quando e , quando e quando . Ou seja, quando os dois são negativos, um é positivo e o outro é negativo e quando os dois são positivos! Vamos lá!
Obs.: quando trocamos o sinal do módulo, trocamos o sinal dele todo! Repare que trocamos o por em algum momento!
Passo 4
Então, vamos usar o e , primeiro:
Essa é a função para os valores a partir do .
Agora, faremos :
Essa é a função para os entre e .
Para os menores que , faremos :
Essa é a função para os valores menores que .
Agora, é só juntar essas três informações! No fim do dia, temos que:
Prontinho!
Resposta
(a)
(b)