Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.2 - Ex. 6
6 ) Seja , onde . Desenhe F(x, y, z),com
Passo 1
Para resolver essa questão temos que entender como é a interpretação de Gradiente. Quando definimos a reta normal de uma superfície qualquer – S
OU seja o vetor normal é o Gradiente com modulo 1. Assim eles tem o mesmo comportamento.
Passo 2
No nosso caso que nossa superfície é uma casca esférica, o Gradiente vai ser uma infinidade de vetores que tem formato radial. Vou te provar
E Gradiente tem o formato
Assim o gradiente da esfera tem o seguinte vetor
Passo 3
A interpretação geométrica pode ser observada abaixo
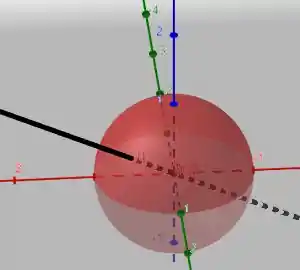
Onde a reta preta é o gradiente. Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
É dado uma tabela com valores de uma função f com gradiente contínuo. Determine ∫ C ∇ f ⋅ r → , onde C tem equações paramétricas x = t 2 + 1 , y = t 3 + t, 0 ≤ t ≤ 1
Determine se F → é ou não um campo vetorial conservativo. Se for, determine uma função f tal que F → = ∇ f F → x , y = 2 x - 3 y i → + - 3 x + 4 y - 8 j →
A partir do gráfico de F → você diria que o campo é conservativo? Explique.
Este exercício ilustra a relação entre o vetor rotacional e rotações. Seja B um corpo rígido girando em torno do eixo z . A rotação pode ser descrita pelo vetor ω → = ω k → , onde ω é a velocidade ang
Determine (a) o rotacional e (b) o divergente do campo vetorial. F x , y , z = 1 x 2 + y 2 + z 2 xi + yj + zk