Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.3 - Ex. 4
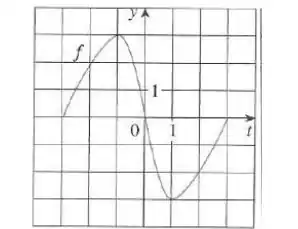
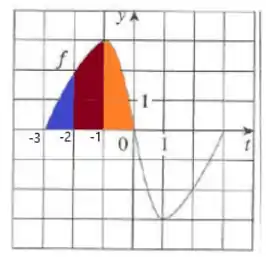
Seja onde é a função cujo gráfico é mostrado.
(a) Calcule e .
(b) Estime , e .
(c) Em que intervalo está crescendo?
(d) Onde tem um valor máximo?
(e) Faça um esboço de gráfico de .
(f) Use o gráfico da parte (e) para esboçar o gráfico de . Compare com o gráfico de .
Passo 1
Fala aí! tudo certinho?
Nesse problema temos um gráfico de e .
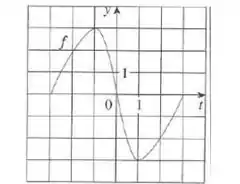
A partir daí a questão pede para calcularmos e , estimar , e , encontrar o intervalo onde é crescente e o seu ponto máximo. Além disso queremos esboçar o gráfico de e .
Bastante coisa, não é?
Para resolver esse problema vamos dar uma olhadinha em:
Perceba que é a integral de , podemos dizer então que e a área abaixo da curva de entre e .
Então para calcular , , , e , aplicamos em e analisamos a area abaixo de .
A partir daí podemos estimar também o intervalo onde é crescente e o ponto máximo e estimar os gráficos de e .
Para usamos a propriedade que diz:
Bora começar!
Passo 2
Primeiro vamos calcular e .
Como e a integral dá a área do gráfico, temos para :
Como os limites de integração são os mesmos, a área abaixo de ente e é , logo:
Agora para , temos:
Olhando para o gráfico de , vemos que é uma função ímpar, então a área abaixo de entre e é igual a área abaixo de entre e ... com isso, podemos dizer que uma área cancela a outra, portanto pela simetria:
Tranquilo até aqui?
Passo 3
Agora vamos estimar , e a partir de uma estimativa de área.
Para :
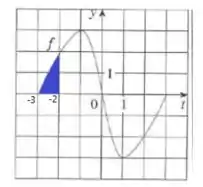
Para temos que a área está próxima à área do triângulo de base e altura de modo que:
Para , vamos fazer a mesma análise:
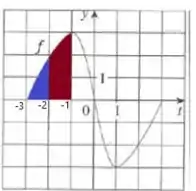
Podemos escrever como:
O valor de já temos e a área abaixo de entre e pode ser aproximada pela área de um trapézio de altura , base maior e base menor .
Show?
Passo 4
Para estimar , fazemos:
Ou seja:
O valor de já temos, e a área abaixo de entre e pode ser aproximado por um triangulo de base e altura .
Bacana, não é?
Passo 5
Para determinar o intervalo crescente de temos que lembrar que é a área abaixo de . Ou seja, está crescendo em pois com o crescimento de nesse intervalo, nós continuamos adicionando mais área. A partir de a área está abaixo do eixo , então a área é negativa, então descresce.
Portanto, Temos máximo no momento em que não temos mais adição de área e passamos a ter subtração de área, ou seja, temos máximo em .
Maravilha!
Passo 6
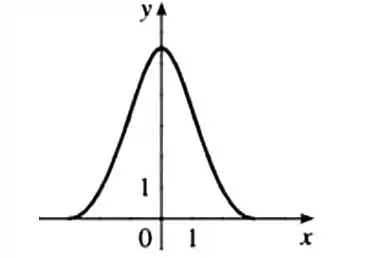
Esboçando o gráfico de , a partir do que discutimos no passo anterior, temos:
Estamos quase no fim!
Passo 7
Para determinar o gráfico de , temos que lembrar da propriedade do teorema fundamental do cálculo:
Então se:
Temos que:
O gráfico de é o mesmo gráfico de . Isso confirma o Teorema fundamental do cálculo.
É isso! O que achou? Responde Aí!
Resposta
(a) e
(b) , e
(c) está crescendo em .
(d) máximo em .
(e)
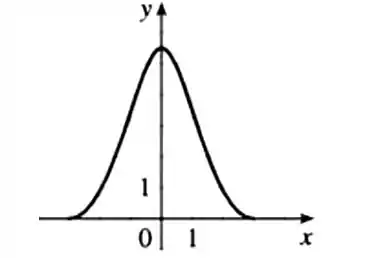
(f) O gráfico de é o mesmo gráfico de .