Seja o operador diferencial linear definido por

Em que são constantes reais.

(a) Encontre .

(b) Encontre .

(c) Determine quatro soluções da equação . Você acha que essas quatro soluções formam um conjunto fundamental de soluções? Por quê?

Nosso próximo passo será aplicar a função . As derivadas são:

Aplicando ao operador diferencial:

O item (c) nos pede para determinar as soluções da equação:

E verificar se elas formam um conjunto fundamental de soluções. Vamos lá???

Como temos uma equação linear homogênea uma possível solução do problema é . As derivadas da função são:

Aplicando na equação:

Vamos dizer que . Ficamos com:

Então, as soluções para a equação são:

Para dizer se as funções formam um conjunto fundamental de soluções devemos agora calcular o wronskiano. Ele é dado por:

O determinante da matriz em que cada coluna representa uma função solução e cada uma das suas derivadas até uma ordem a menos que a ordem da equação diferencial. Como nossa equação diferencial era de quarta ordem, nosso wronskiano deve ir até a terceira derivada. Tudo bem???

Então, nosso wronskiano é:

Multiplicando todas as linhas por ficamos com:

Para calcular o determinante precisamos reduzir a matriz para uma ordem menor. Para isso vamos aplicar a regra de Chió. Ela é dada por:

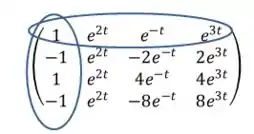
Encontramos um coeficiente igual a 1. Então selecionamos a linha e a coluna do coeficiente. Dos termos que restaram devemos subtrair a multiplicação dos termos correspondentes na linha e coluna que retiramos. Vamos fazer pegar um termo para exemplificar:

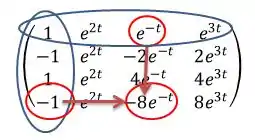
O termo na matriz original é . Na coluna em que ele estava retiramos o número e, na linha em que ele estava retiramos o número -1. Tudo bem???

Na matriz reduzida este termo será . Fez sentido agora? Vamos então determinar a matriz reduzida:

Agora que temos uma matriz 3x3 podemos calcular o determinante:

Como o wronskiano não se anula, as funções formam conjunto fundamental de soluções.