Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.4 - Ex. 46
- Seja P um ponto fora do plano que passa pelos pontos Q, R e S. Mostre que a distância de P para o plano é
Onde .
- Use a fórmula da parte (a) para encontrar a distância do ponto em relação ao plano que passa pelos pontos , e .
Onde .
Passo 1
- Vamos dar uma olhada numa figura pra orientar a gente...
- Vamos identificar os lados fazendo os vetores. A gente tem que:
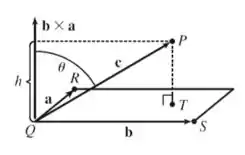
A distância do ponto P ao plano é , nessa figura a gente tá demarcando como o segmento .
A gente sabe que é perpendicular a , então, é paralelo a .
é também a projeção escalar de sobre , ou seja .
Sendo o volume e a área da base do paralelepípedo gerado pelos vetores.
Então,
Passo 2
Então...
A gente quer achar , então precisamos:
Vamos encontrar o produto misto...
Agora só falta o produto vetorial de ...
E...
Passo 2
A distância então é:
Resposta
Exercícios de Livros Relacionados
Calcule | u → ^ v → | , sabendo que u → = 4 , v → = 13 e u → ⋅ v → = 48 .
Sendo w → = ( u → + 2v → ) ^ ( u → + v → ) , determine o ângulo dos vetores u → e v → , sabendo que u → = v → = w → = 2 e u → ⋅ v →0 .
Determine a área do paralelogramo ABCD cujas diagonais são A C → = 0,2 , 3 e B D → = - 2,4 , 1 .
Sendo u → = - 1,1 , m ,v → = 7,5 , 1ew → = a , b , c , pede-se:O valor de m para que a equação v → = u → ^ w → possa ter solução;Para o valor de m encontrado em a), resolva a equação v → = u → ^ w → ,
Dados u → = ( 1,2 , - 1 ) e v → = ( 1,3 , - 2 ) , determine um vetor a → , ortogonal a u → e a v → , de módulo 3 e que forma com k → um ângulo obtuso.