Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 39
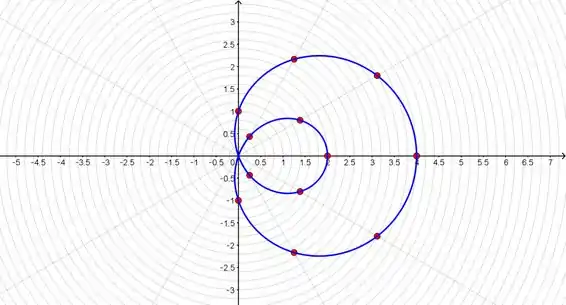
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
Primeiro faremos o gráfico cartesiano com a modificação acima. Utilizaremos o GeoGebra para plotarmos o nosso gráfico.
Já para encontrarmos o gráfico no plano polar, o que iremos fazer é criar uma tabela com os valores de e de , assim poderemos acompanhar, em conjunto com o gráfico cartesiano, o movimento da nossa curva.
Com auxílio do Desmos, iremos plotar os pontos e assim teremos o nosso gráfico. Veja que ao plotarmos o gráfico no eixo coordenado, iremos utilizar os pontos que plotamos na hora de criarmos o gráfico no plano polar, então analisar o comportamento oscilatório e a frequência da função no plano coordenado é importante.
Passo 2
Com o GeoGebra a gente tem o gráfico de
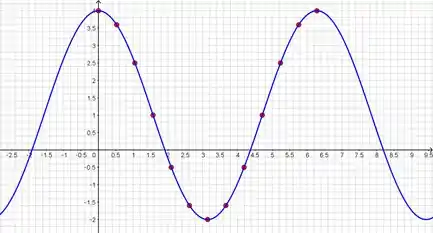
Temos então o gráfico da função com amplitude e deslocado para cima em uma unidade. A função tem ainda o período de .
Passo 3
Criando nossa tabela:
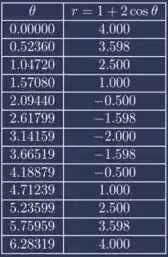
Agora poderemos utilizar o desmos para colocar os pontos e traçarmos nossa figura:
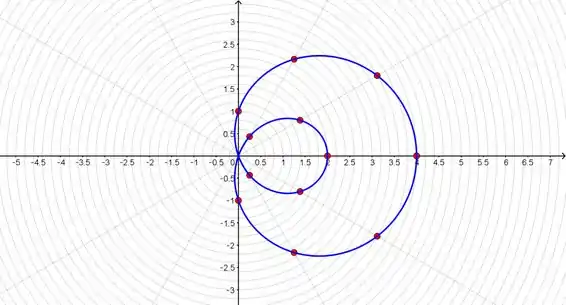
Resposta
