Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.4 - Ex. 45
- Seja um ponto não pertenente à reta que passa pelos pontos e . Mostre que a distancia do ponto até a reta é
Onde e .
- Utilize a fórmula da parte do exercício para determinar a distância do ponto à reta que passa por e
Onde e .
Passo 1
Primeiramente, vamos tentar desenhar tudo isso aí que a questão falou pra gente:
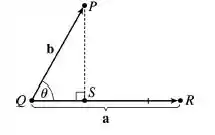
Repare que pela nossa figura, podemos dizer que a distancia entre o ponto e a reta que ta na direção do vetor é dada por
E se você reparar também, existe um triangulo retângulo ali na nossa figura! E dele, podemos tirar que:
Tudo certo até aqui?
Show!
Passo 2
Acontece que a fórmula onde queremos chegar é essa aqui
Que é uma parada que envolve produto vetorial.
E o que temos até agora é uma parada que envolve seno.
Então vamos lembrar o seguinte:
Isolando o seno:
Passo 3
Agora igualando as duas fórmulas que temos:
E chagamos na fórmula que a gente queria
Passo 4
Para determinar a distância do ponto à reta que passa por e , vamos definir:
Passo 5
Agora, vamos calcular :
Passo 6
Calculando :
Passo 7
Substituindo tudo na fórmula da letra :