O índice de temperatura-umidade (ou simplesmente humidex) é a temperatura aparente do ar quando a temperatura real é e a umidade relativa é , de modo que podemos escrever . A tabela seguinte com valores de foi extraída de uma tabela do Environment Canada.

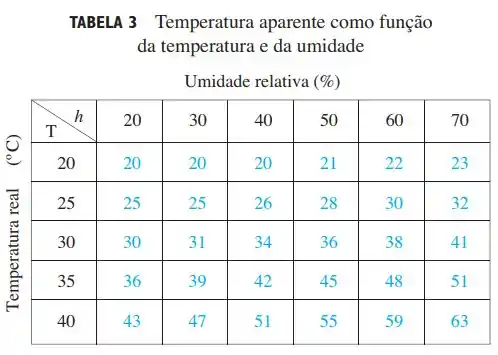
(a) Qual é o valor de ? Qual é o seu significado?

(b) Para que valor de temos ?

(c) Para que valor de temos ?

(d) Qual o significado de e ? Compare o comportamento dessas duas funções de .

Veja que nesse ponto temos e . Desse modo, o valor correspondente a será dado pelo cruzamento da linha correspondente a essa temperatura com a coluna correspondente a essa umidade relativa:

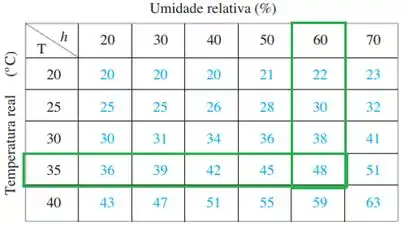
Assim, encontramos:

Isso significa que a uma temperatura de e uma umidade relativa de o índice de temperatura-umidade é , isto é, a temperatura aparente do ar é de

(b) Aqui queremos saber para qual valor de teremos .

Para saber isso, devemos analisar a linha que corresponde a uma temperatura e encontrar o valor 36. Esse valor de temperatura aparente do ar estará na coluna de umidade relativa, e nos dará o correspondente.

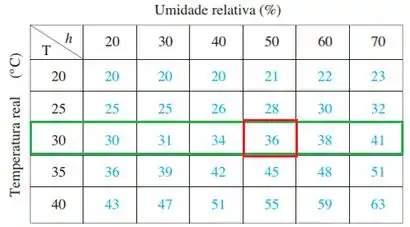
Olhando a tabela acima, vemos que o 36 está na coluna onde . Portanto, a uma temperatura de e umidade relativa de a temperatura aparente do ar é de

(c) Aqui queremos saber para qual valor de teremos

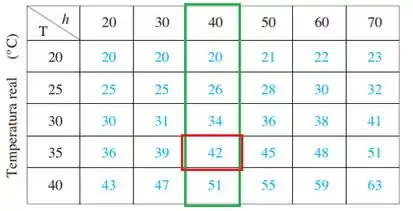
Aqui vamos olhar a tabela acima analisando a coluna cuja umidade relativa é . Vemos que o valor de temperatura aparente do ar 42 encontra-se na linha da temperatura

(d) Para temos o índice em função da umidade relativa a uma temperatura constante de . Para temos o índice em função da umidade relativa a uma temperatura constante de .

Para temos uma função crescente que nas primeira colunas de umidade não muda, mas nas ultimas aumenta a uma taxa pequena, para temos uma função linear crescente com taxa igual a .