Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 78
- Use o exercício 77 para mostrar que o ângulo entre a reta tangente e a reta radial é em cada ponto na curva .
- Ilustre a parte traçando, com uma ferramenta gráfica, a curva e a reta tangente aos pontos onde e .
- Demonstre que qualquer curva polar com a propriedade de que o ângulo entre a reta radial e a reta tangente é uma constante deve ser do tipo , onde e são constantes.
Passo 1
Eaee, belezinha??? Bom... queremos utilizar o exercício anterior (questão 77) para mostrar que o ângulo entre a reta tangente e a reta radial é em cada ponto na curva .
Para isso, lembre-se que:
Ou seja, a tangente entre o ângulo entre a reta tangente e a reta radial é dada pela razão entre e a derivada de em relação a
Em seguida, utilizando uma ferramenta gráfica, vamos traçar a curva e a reta tangente aos pontos onde e .
Por fim, queremos demonstrar que qualquer curva polar com a propriedade de que o ângulo entre a reta radial e a reta tangente é uma constante deve ser do tipo:
Onde e são constantes.
Aah... como estamos trabalhando com tangentes (e, portanto, derivadas) em coordenadas polares, precisamos ter em mente a seguida expressão da derivada:
Passo 2
Vamos começar pela letra (a).
O enunciado nos disse que:
Então, fazendo a derivada de em relação a , temos:
Assim, substituindo na equação do exercício anterior:
E o ângulo cuja tangente é é , logo:
Passo 3
(b)
Traçando a curva com uma ferramenta gráfica, temos:
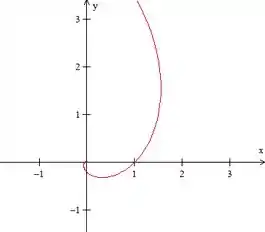
Passo 4
Agora vamos achar as equações das retas tangentes nos pontos correspondentes a e .
A inclinação da reta tangente é dada por:
Assim, aplicano a derivada, temos:
Quando , temos:
E quando , temos
Passo 5
Além disso precisamos descobrir quando valem e quando e .
Lembrando que podemos relacionar as coordenadas cartesianas com as polares utilizando a seguinte conversão:
Então, quando , temos:
E quando , temos
Passo 6
As equações das retas tangentes são dadaas por:
Onde é um ponto conhecido.
No nosso caso, temos o ponto , portanto:
Obs: lembre-se que aqui .
E, para o ponto , temos:
Obs: lembre-se que aqui .
Passo 7
Traçando essas duas retas junto com o gráfico que traçamos no passo 3:
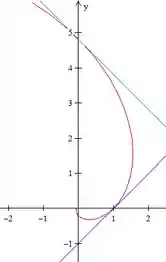
Passo 8
(c)
Vamos chamar:
Assim,
E temos uma EDO separável para resolver.
Passo 9
Pra resolver isso, multiplicando cruzando:
Integrando de ambos os lados:
Resolvendo as integrais:
Lembrando que é uma constante.
Falando em constante, vamos juntar as constantes e vamos isolar o :
E se a gente chamar e ficamos com a mesma notação da questão e chagamos exatamente onde ela nos pediu:
Resposta
- Demonstração.
-
- Demonstração.