Seja . Represente geometricamente , sendo
Passo 1
O gradiente de é definido como
Calculando as derivadas
Então o gradiente é dado por
No ponto
Passo 2
Representando no plano o vetor saindo do ponto :
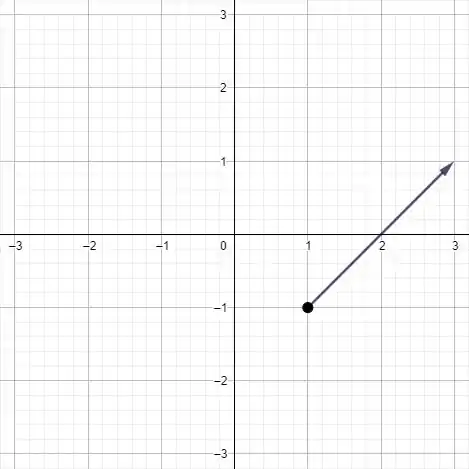
Resposta
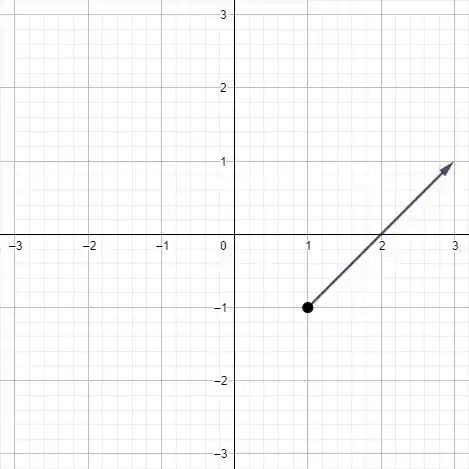
Seja . Represente geometricamente , sendo
O gradiente de é definido como
Calculando as derivadas
Então o gradiente é dado por
No ponto
Representando no plano o vetor saindo do ponto :

