Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.5 - Ex. 5
Seja e seja uma curva diferenciável cuja imagem está contida na curva de nível , isto é, para todo no domínio de , , (dê exemplo de tal curva). Seja . Prove que . Interprete geometricamente.
Passo 1
A curva é definida pela curva de nível , que é a circunferência , tal curva é parametrizada como .
Precisamos provar que , para isso precisamos calcular a derivada de e o gradiente de .
Derivando
E as derivadas de
E o gradiente
Passo 2
No ponto temos , mas sabemos que , então
Na derivada , quando
E o gradiente no ponto
Calculando então o produto escalar
Passo 3
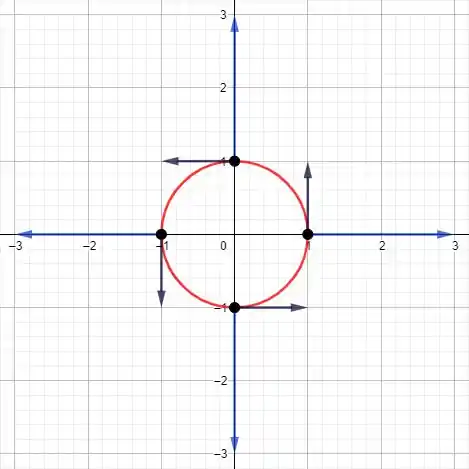
Quando o produto escalar é zero, os vetores aplicados são ortogonais. Podemos provar geometricamente, jogando os vetores no plano, onde os vetores mais escuros são e os mais claros .
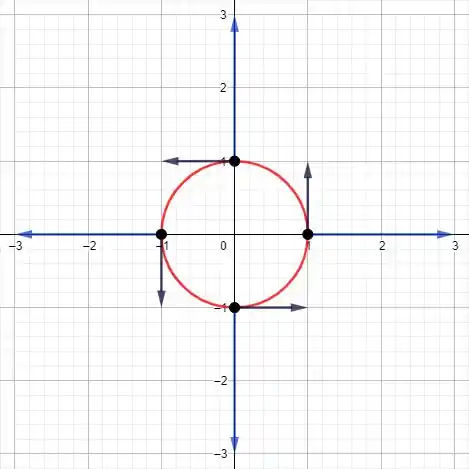
Podemos perceber que para cada vetor existe um vetor que é perpendicular.
Resposta
