Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.7 - Ex. 11
Seja , .
- Estude o sinal de .
- Faça um esboço do gráfico de .
Passo 1
- Vamos analisar a função, vamos ter então que usar a fórmula da função trigonométrica para achar :
- Vamos fazer um esboço do gráfico da função:
Agora é só aplicar, vamos lá?
Passo 2
Vamos agora estudar o sinal de :
Temos então que quando:
Podemos ver no círculo trigonométrico abaixo que do ângulo até chegar a , e acontece novamente de até e entre e :
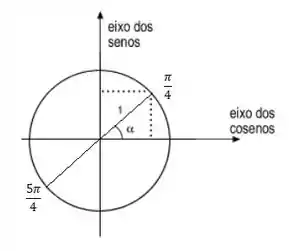
Assim, quando:
e
E :
Passo 2
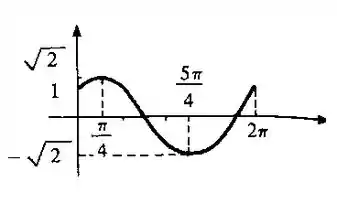
Resposta
- em e , em
Exercícios de Livros Relacionados
Encontre f ' ( a ) . f x = 3 x + 1
Cada limite representa a derivada de certa função f em certo número a . Diga quem é f e a em cada caso. lim h → 0 1 + h 10 - 1 h
Cada limite representa a derivada de certa função f em certo número a . Diga quem é f e a em cada caso. lim h → 0 cos π + h + 1 h
Uma lata de refrigerante morna é colocada na geladeira. Esboce o gráfico da temperatura do refrigerante como uma função do tempo. A taxa de variação inicial da temperatura é maior ou menor que a taxa
Cada limite representa a derivada de certa função f em certo número a . Diga quem é f e a em cada caso. lim t → 1 t 4 + t - 2 t - 1