Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.3 - Ex. 46
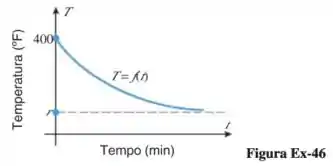
Seja a temperatura de uma batata cozida minutos depois de retirada de um forno quente. A figura abaixo mostra a curva da temperatura versus tempo para a batata, onde denota a temperatura ambiente.
a) Qual é o significado físico de ?
b) Qual é o significado físico de ?
Passo 1
a) Então pessoal, se observarmos com cuidado o gráfico que o enunciado nos cedeu, fica tranquilo concluirmos que quando , ou seja, quando o tempo tende a zero pela direita, a temperatura da batata é exatamente a maior temperatura que ela poderia atingir cozinhando! Oras, faz sentido, não é? No tempo é o momento em que a batata possui maior temperatura, uma vez que acabou de sair do forno! De acordo com a curva, temos:
Essa é a temperatura inicial da batata após ser retirada do forno, esse é o significado físico do limite acima, gente!
Passo 2
b) Diferentemente da questão anterior, por conta dos princípios físicos da termodinâmica, para um tempo infinitamente grande a tendência do sistema em questão vai ser igualar a temperatura da batata com a temperatura do ambiente, e é exatamente por isso que aparece uma assíntota em , que é justamente essa temperatura ambiente. Sendo assim, de acordo com a curva, temos:
Essa é a temperatura final e limite da batata após ser retirada do forno, esse é o significado físico do limite acima! 😊
Resposta
a)
Se trata da temperatura inicial da batata.
b)
Se trata da temperatura final e limite da batata.