Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 5
Seja o volume do sólido que se encontra abaixo do gráfico de e acima do retângulo dado por , . Use as linhas e para dividir em sub-retângulos. Sejam e as somas de Riemann calculadas usando os cantos inferiores esquerdo e superior direito, respectivamente. Sem calcular os números , e , organize-os em ordem crescente e explique seu raciocínio.
Passo 1
E ai, pessoal, beleza?
Essa questão pede pra gente comparar as somas de Riemann calculadas nos cantos inferior esquerdo e superior direito dos sub-retângulos ( e ) entre si e com o volume do sólido ().
Pra isso, vamos lembrar a soma de Riemann:
Além disso, o volume é calculado pela soma de Riemann com
Para ordenar esses três valores sem calcular, vamos primeiro comparar e , e depois comparar os dois com o .
Passo 2
Vamos comparar e observando o valor da função nos pontos amostrais de cada uma das somas de Riemann. Vamos ver então o exemplo de um sub-retângulo:
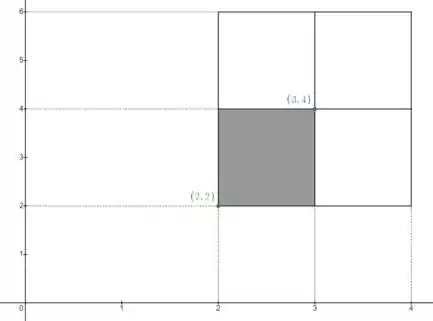
O ponto azul se refere à soma , enquanto o ponto verde se refere a . Percebemos que tanto o valor de quanto de do ponto de são menores que de .
Agora voltando à função:
Nessa função, quanto maiores os valores de e , menor vai ser o valor de . Como estamos em um domínio no primeiro quadrante ( e são positivos), isso quer dizer que quanto maiores os valores de e , menor o valor de .
O que a gente conclui com isso?
Bom, de os pontos amostrais de têm valores maiores para e , os cálculos de nesses pontos serão menores, portanto, a soma de Riemann vai dar um valor menor!
Vamos observar isso pro sub-retângulo que a gente viu:
Como , aconteceu exatamente o que a gente concluiu!
Ou seja,
Passo 3
Para comparar o com essas somas, vamos definir o volume como o limite da soma de Riemann, usando a regra do ponto médio:
E essa soma usando o ponto médio vai ser a melhor aproximação para o volume!
Vamos entender porque, voltando para o nosso sub-retângulo do exemplo:
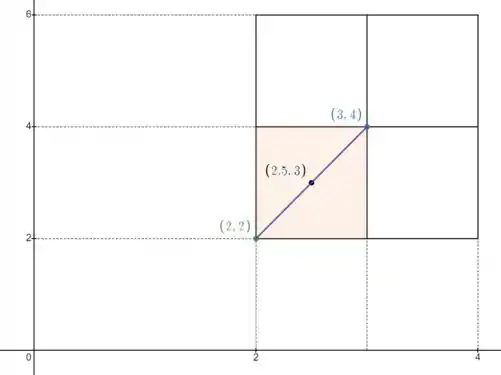
Percebe que o ponto onde a função admite seu valor máximo nesse sub-retângulo é o , e o valor mínimo é no ponto . Isso quer dizer que a soma está superestimando o volume do sólido, enquanto a soma está subestimando.
A melhor aproximação, então, vai ser alguma coisa entre esses dois valores, calculando um ponto entre os dois (ponto médio, nesse caso, o ).
Qual vai ser a conclusão então?
Bom, vimos que os pontos onde calculamos a melhor aproximação para estão entre os pontos de e , ou seja: