Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 9
Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Passo 1
Eaiii pessoal, tudo bem com vocês?
Bom, vamos começar entendendo o enunciado, beleza?
Precisamos calcular a integral dupla definida na região , identificando como um volume de um sólido.
Como fazer isso?Vamos interpretar essa integral como o volume que está abaixo do plano e acima do retângulo .
Logo, para calcular o volume multiplicamos base vezes largura vezes altura. Agora, é só você identificar essas coordenadas, e para isso é interessante fazer um esboço das regiões, pois vai ajudar.
Seu gráfico vai ficar com essa cara, onde a região está representada pela retângulo de coordenas , e o plano pelo retângulo de coordenadas . Agora ficou fácil calcular o volume né!?
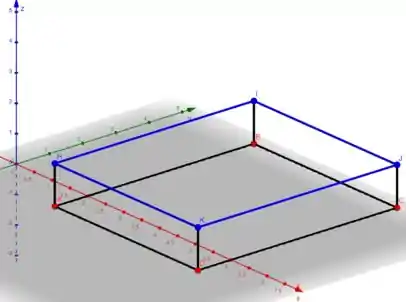
Partiu fazer esses passos! Bora lá!!!
Passo 2
Galera, primeiro vamos esboçar nossas regiões.
Sabemos que, é um retângulo no plano e é um plano.
Observe o gráfico:
- Temos o retângulo ABCD nos intervalos de e ;
- E o plano sobre ele;
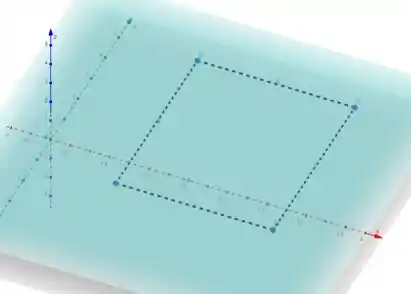
Passo 3
Sabendo disso, vamos calcular o volume entre eles agora.
A área do retângulo é:
A é , e mede .
A é y, e mede 6.
Logo, nossa área fica:
A altura é a distância no eixo , ou seja, do ponto zero até o plano
Então, a altura em é .
Assim, integral pode ser calculada:
Logo,
Prontinho!