Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.1 - Ex. 25
Sejam a área entre o gráfico de e o intervalo ; e a área entre o gráfico de e o intervalo . Explique geometricamente por que .
Passo 1
Bom, a área entre os gráficos, usando o Geogebra seria:
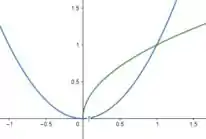
Como podemos ver, também é a área entre o gráfico de e o intervalo no eixo . Portanto, é a região de encontro das duas funções, que é localizado no ponto .
Certinho??
Resposta
é a região de encontro das duas funções, que é localizado no ponto .
Exercícios de Livros Relacionados
Use as regras na Tabela 5.4 e as Equações 1 e 3 para calcular as integrais dos Exercícios 41-50.41 ∫ 3 1 7 d x
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.37 ∫ a 2 a x d x
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.36 ∫ 0 π 2 ѳ 2 d ѳ ѳ ѳ
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.40 ∫ 0 3 b x 2 d x
Use as regras na Tabela 5.4 e as Equações 1 e 3 para calcular as integrais dos Exercícios 41-50.42 ∫ 0 2 2 t - 3 d t