Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.1 - Ex. 2

2 ) Sejam γ1 a poligonal de vértices A, B, C, D orientada no sentido antihorário e γ2 a poligonal de vértices H, G, F, E orientada no sentido horário.

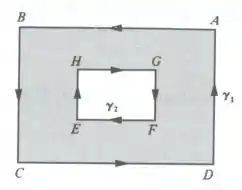
Suponha P e Q de classe C1 num aberto contendo K, onde K é a regiãocompreendida entre as poligonais. Prove que

Passo 1

Para resolver essa questão vamos precisar usar um argumento geométrico, vamos pegar nossa região e dividir em 2

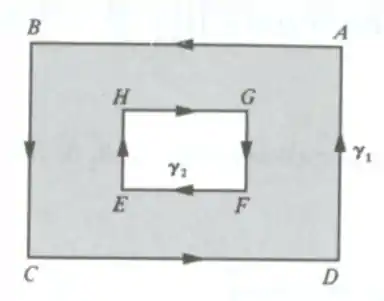
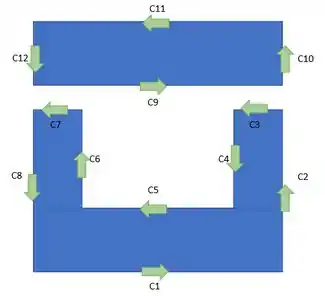
Passo 2

Se aplicarmos o teorema de Green nas duas regiões veremos que

Passo 3

Se formos observar C7, C3 estão na mesma reta que C9 contudo estão em direções contrarias, Logo eles vão se cancelar parcialmente. E se formos Somar as Curvas 1 ,2 ,10,11,12,8 formam um ciclo fechado com orientação anti-horaria que o enunciado Chama de . E o mesmo raciocínio serve para o Conjunto de Curvas 3,4,5,6,7,9 formam uma curva horaria que o enunciado chama de Logo podemos ver que

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aplique o teorema de Green para calcular as integrais nos Exercí-cios 21-24 ∮ C ( 6 y + x ) d x + ( y + 2 x ) d y C : A circunferência ( x - 2 ) 2 + ( y - 3 ) 2 = 4 .

Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = x 3 y 2 i + 1 2 x 4 y j

Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = x y + y 2 i + ( x - y ) j

Encontre a circulação em sentido anti-horário e o fluxo exterior do campo F = xyi + y2j ao redor e sobre a fronteira daregião delimitada pelas curvas y = x2 e y = x no primeiro quadrante

Utilize a fórmula da área do teorema de Green fornecida acima para encontrar as áreas das regiões delimitadas pelas curvas nos Exercícios 25-28A circunferência r(t) = (a cos t)i + (a sen t)j, 0 ≤ t ≤