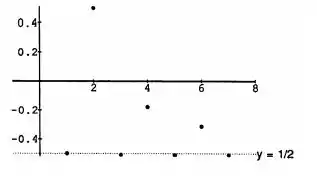
Na série harmônica alternada, suponha que o objetivo seja rearranjar os termos para conseguir uma nova série que convirja para -1/2. Inicie o novo rearranjo com o primeiro termo negativo, que é -1/2. Sempre que você tiver uma soma que seja menor ou igual a -1/2, comece a introduzir termos positivos, tomados em ordem, até que o novo total seja maior que -1/2.
Em seguida, adicione termos negativos até que o total seja menor ou igual a -1/2 novamente. Continue esse processo até que suas somas parciais estejam acima do objetivo ao menos três vezes e finalize aí ou abaixo dele. Se for a soma dos primeiros n termos de sua nova série, marque os pontos para ilustrar como as somas estão se comportando.
Passo 1
Iaiii galera, espero que estejam bem! Vamos lá pra mais uma questão de Sequências Infinitas e Séries!
Essa é uma daquelas questões que não tem jeito, precisamos colocar a mão na massa haha!
Comecemos definindo a coordenada de cada ponto.
Passo 2
Ufa! Ainda seguindo a mesma lógica temos
Passo 3
E agora, só precisamos dispor essas coordenadas encontradas em um plano cartesiano.
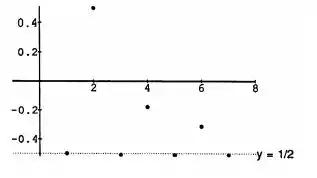
Resposta