Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.4 - Ex. 2
Use o Teorema de Pitágoras para encontrar o comprimento do segmento de reta de entre e confirme que o valor está de acordo com o comprimento calculado usando:
- Fórmula (4)
- Fórmula (5)
Passo 1
Opaa! Tudo joia?
Olha só, pra começar a gente tem que calcular o comprimento utilizando o Teorema de Pitágoras?
Mas pera...
Teorema de Pitágoras? Cateto? Hipotenusa? Triângulo? What?
Vamos entender isso melhor fazendo o desenho dessa reta no intervalo dados pelos pontos :
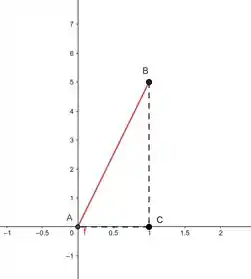
Aaahh agora faz mais sentido! Em vermelho ali é a nossa reta sendo marcada pelos nossos pontos , aí formamos um triângulo e vamos poder aplicar o Teorema de Pitágoras!
Passo 2
Bom, a nossa reta ali representa a hipotenusa, certo?
Então fica assim:
Pela própria figura dá pra a gente ver o tamanho de :
Opaa! Então achamos o comprimento da nossa reta no intervalo ali. O comprimento é
Passo 3
- Beleza, agora a gente vai calcular esse comprimento pela fórmula , que é essa aqui:
- Agora a gente vai usar a fórmula , que é:
Bom, nossa , então:
E o intervalo é em , que vai de .
Nossa integral então é:
Olha só! Achamos o mesmo resultado de cima, então tá certinho!
Passo 4
Então aqui a gente vai ter que jogar nossa função pra .
Olha só, é o mesmo que , certo?
Então podemos escrever:
E aí colocamos nossa função como:
Derivando...
E aqui o intervalo vai ser em , ou seja, de .
Aplicando na fórmula:
E conferiu também! Então nosso comprimento tá certinho, e é mesmo😉