Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 23

Um silo será construído (sem sua base) na forma de um cilindro sob um hemisfério. O custo da construção por unidade de área da superfície é duas vezes maior para o hemisfério em relação à lateral do cilindro. Determine as dimensões para um volume fixo com custos de produção minimizados. Ignore a espessuira do silo e o desperdício na construção.

Passo 1

Peguei uma imagem desse silo para olharmos com calma:

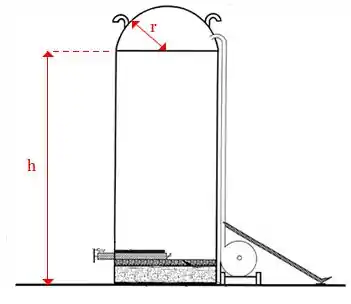
O custo da contrução depende apenas da área lateral e da área do hemisfério. Mas o custo que acharmos da área lateral vai ser metade da do hemisfério.

Usando h par aaltura do cilindro e r para o raio da esfera e do cilindro, vamos ter:

G = A l 2 + A h

Com

A l = 2 π r h

A h = 2 π r 2

A área vai ficar:

G = π r h + 2 π r 2

Ele disse que o volume é fíxo, que vai ser:

V = 2 π r 3 3 + π r 2 h

Isolando o h , vamos ter:

h = V π r 2 - 2 r 3

O gasto vai ficar:

G = π r V π r 2 - 2 r 3 + 2 π r 2

G = V r - 2 π r 2 3 + 2 π r 2

G = V r + 4 π r 2 3

O valor de r pode ir de 0 , até quando não temos altura e o volume do hmesfério é V

V = 2 π r 3 3

r = 3 V 2 π 3

Então:

0 ≤ r ≤ 3 V 2 π 3

Passo 2

Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.

Começando por achar os pontos críticos:

G = V r + 4 π r 2 3

Vamosescrever aquela primeira fração como potência

G = V r - 1 + 4 π r 2 3

Assim:

G ' = - V r - 2 + 8 π r 3

Fazendo isso igual a 0

- V r - 2 + 8 π r 3 = 0

V r 2 = 8 π r 3

Multiplicando cruzado:

3 V = 8 π r 3

r 3 = 3 V 8 π

r = 3 V 8 π 3

Passo 3

Vamos achar o valor da função nos pontos críticos e extremos do intervalo:

G = V r + 4 π r 2 3

Vamos ter:

r = 0 → G = V 0 + 4 π 0 2 3 = ∞

r = 3 V 8 π 3 → G = V 3 V 8 π 3 + 4 π 3 V 8 π 3 2 3 = 3 V + 4 π 3 V 8 π 3 3 V 8 π 3 = 3 V + V 2 3 3 V 8 π 3 = 7 V 2 3 3 V 8 π 3 = 7 V 6 8 π 3 V 3

r = 3 V 2 π 3 → G = V 3 V 2 π 3 + 4 π 3 V 2 π 3 2 3 = 3 V + 4 π 3 V 2 π 3 3 V 2 π 3 = 3 V + 6 V 3 3 V 8 π 3 = 9 V 3 3 V 8 π 3 = 3 V 2 π 3 V 3

O maior dos 3 valores é quando r = 3 V 8 π 3

Suas dimensões serão

r = 3 V 8 π 3

E

h = V π 3 V 8 π 3 2 - 2 3 V 8 π 3 3 = 3 V π 3

Resposta

r = 3 V 8 π 3

E

h = 3 V π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A soma de dois números não negativos é 20. Diga quais serão esses númerosSe o produto de um número multiplicado pela raiz quadrada de outro tiver que ser o maior possível.
Determine a altura e o raio do maior cilindro circular reto que pode ser colocado dentro de uma esfera de raio 3 .
A soma de dois números não negativos é 20. Diga quais serão esses númerosSe a soma de um número com a raiz quadrada do outro tiver que ser a maior possível.
Um triângulo isósceles tem seu vértice na origem, e sua base é paralela ao eixo x, estando os vértices da base acima do eixo, sobre a curva y = 27 - x 2 . Determine a maior área que o triângulo pode a
Um cliente lhe pediu que projetasse um tanque retangular de aço inoxidável, sem tampa. Ele deverá possuir base quadrada e um volume de 32 pés e será soldado a partir de chapas de aço com espessura de