Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.6 - Ex. 72

Simplifique a expressão

sin (2 cos^(- 1) (x))

Passo 1

Opa, bora lá! Temos que simplificar a expressão:

sin (2 cos^(- 1) (x))

A primeira coisa que vamos fazer é usar a identidade trigonométrica:

sin (2 theta) = 2 sin (theta) cos (theta)

Assim:

sin (2 cos^(- 1) (x)) = 2 sin (cos^(- 1) x) cos (cos^(- 1) x)

Passo 2

Agora devemos lembrar que para as funções inversas o raciocínio deve ser o inverso do que fazemos com a função normal, ou seja, devemos pensar qual é o arco (ângulo) cuja função da o resultado entre parênteses.

2 sin (cos^(- 1) x) cos (cos^(- 1) x)

Pra a gente sair dessa a gente tem que entender que sin (cos^(- 1) x) e cos (cos^(- 1) x) estão relacionadas pelo teorema de Pitágoras, assim:

y = cos^(- 1) (x) -> cos (y) = x

Vamos interpretar essa função inversa da forma geométrica pra ficar mais fácil:

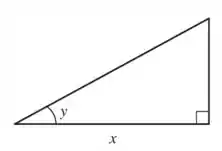
Assumindo a hipotenusa como 1 podemos determinar pelo teorema de Pitágoras:

1^2 = x^2 + sin^2 y

sin y = sqrt(1 - x^2)

Assim:

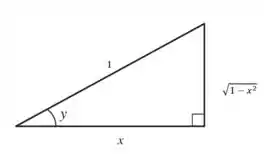
Passo 3

Substituindo na expressão original:

2 sin (cos^(- 1) x) cos (cos^(- 1) x) = 2 sin (y) cos (y) = 2 (sqrt(1 - x^2)) (x)

Assim:

2 sin (cos^(- 1) x) cos (cos^(- 1) x) = 2 x sqrt(1 - x^2)

Prontinho!

Resposta

2 x sqrt(1 - x^2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o valor exato de cada expressão.(b) sen - 1 ⁡ sen ⁡ 7 π 3
Demonstre que cos ⁡( s e n - 1x ) = 1 - x ² ².
Encontre o valor exato de cada expressão.(b sen ⁡ 2 . sen - 1 ⁡ 3 5 )
Simplifique a expressão sin ⁡ ( tan - 1 ⁡ x )
Obtenha os gráficos das funções dadas em uma mesma tela. Como esses gráficos estão relacionados? y = tan ⁡ x;- π 2 ≤ x ≤ π 2; y = tan - 1 ⁡ x ; y = x