Qual é o sinal das seguintes expressões?
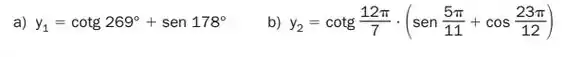
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Para isso vamos estabelecer umas coisinhas.
Sabemos que a função cotangente nada mais é que o logo, basta analisarmos o sinal da tangente e saberemos os da cotangente. Fazendo isso, temos:
Cotangente é positiva no primeiro e no terceiro quadrante e negativa nos demais.
Já a função seno, é positiva nos dois primeiros quadrantes e negativa nos demais.
E por fim, a função cosseno é positiva no primeiro e no quarto quadrante e negativa nos demais.
Passo 2
Agora, com tudo isso em mãos vamos a resolução dos itens.
Item a)
Temos a soma de uma cotangente no terceiro quadrante e um seno no segundo quadrante, a soma de dois termos positivos resulta em um termo positivo, logo:
Item b)
Vamos analisar primeiro os parênteses, dentro dos parênteses temo uma soma de um seno no primeiro quadrante com um cosseno no quarto quadrante, ou seja, a soma de dois termos positivos resulta um termo positivo.
Desse modo, quem ditará o sinal de y é a função cotangente, e está encontra-se no quarto quadrante e é negativa. Logo:
Resposta
a) positiva.
b) negativa.