Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 17.4 - Ex. 12
A solução de problema valor inicial
É chamada de equação de Bessel de ordem .
- Resolva o problema de valor inicial para determinar uma expansão em série de potências da função de Bessel.
- Faça o gráfico de vários polinômios de Taylor até atingir um que pareça uma boa aproximação para a função de Bessel no intervalo de .
Passo 1
Olá, tudo bem? Bom, esse exercício tem como finalidade nos mostrar a equação de Bessel. Ela apresenta a equação de ordem zero, mas podemos encontrar facilmente em ordens superiores. Para resolver vamos começar supondo solução do tipo série de potência:
A derivada em relação à é:
E a derivada segunda é:
Agora vamos substituir na equação diferencial:
E já vamos colocar os termos com que estão do lado de fora dos somatórios para dentro:
Pronto, vamos continuar?
Agora temos uma equação em série de potência, vamos ver como se resolve?
Passo 2
A primeira coisa a ser feita para resolver uma equação diferencial por série de potência é igualar os expoentes dos somatórios. Sempre buscando deixa-los na maior potência de possível. No nosso caso o maior expoente é do terceiro somatório do lado esquerdo, com potência . Então vamos arrumar o primeiro e o segundo somatórios do lado esquerdo.
- O primeiro do lado esquerdo:
- Agora o segundo somatório:
Vamos substituir o índice original por . Assim vamos ter , então o original vai virar :
E agora vamos simplificar os índices:
E por simplicidade podemos trocar o índice por novamente. Aqui é só uma mudança de índice, então o nome não importa efetivamente, apenas as somas =)
Vamos substituir o índice original por :
E agora vamos simplificar os índices:
E por simplicidade podemos trocar o índice por novamente. Aqui é só uma mudança de índice, então o nome não importa efetivamente, apenas as somas =)
E podemos agora podemos substituir novamente na equação diferencial:
Beleza! Agora vamos arrumar os somatórios? =D
Passo 3
Bom, agora que temos todos os com a mesma potência, vamos olhar para o início dos somatórios. Dois deles começam em e outro em , então devemos colocar o primeiro termo do que começa com para fora e assim deixar todos somatórios começando em (sempre deixar com o maior índice comum a todos):
Beleza! Agora que temos os somatórios iguais e as potências de iguais, podemos unir esses dois somatórios em um só:
Para essa sentença ser verdadeira teremos:
Pois do outro lado não temos nenhum polinômio de primeiro grau para igualar, então é nulo.
E também tudo que está dentro dos colchetes no somatório deve ser zero:
Podemos organizar melhor essa expressão:
E daí olha só:
Assim podemos isolar o termo
Agora pare! Antes de ir vendo qual é a fórmula para , vamos aplicar as condições de contorno!
Passo 4
Então é aqui que testamos as condições iniciais. Lá do passo temos:
A primeira condição inicial nos diz que para , então substituindo na solução que supomos lá no começo temos:
Ok! Agora a segunda condição de contorno diz respeito à derivada de . Então, também do passo :
E a condição de contorno nos diz que então:
Assim . Show! Então temos . Agora sim podemos ir para o cálculo de .
Passo 5
Voltando no passo e resgatando a fórmula de recorrência para
E vamos variar o valor de para visualizar a recorrência:
- Para :
- Para :
- Para :
- Para :
Se continuarmos, vamos ver que os termos ímpares serão nulos:
Agora para os termos pares:
Então para os termos pares vamos ter:
Passo 6
Beleza! Agora que encontramos o coeficiente podemos voltar para o passo e substituir na solução:
E essa é a função de Bessel de ordem zero:
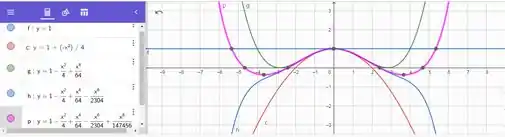
Passo 7
Agora na letra é pedido uma boa aproximação usando os polinômios de Taylor. Eu usei uma calculadora gráfica online e somando os primeiros termos temos (em rosa):
