Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.3 - Ex. 47

∑ n = 1 ∞ 1 n + 1   d i v e r g e  

  1. s 50 = ∑ n = 1 50 1 n + 1 satisfaz ∫ 1 51 1 x + 1 d x < s 50 < ∫ 0 50 1 x + 1 d x . Conclua que 11,5 < s 50 < 12,3 .

  2. Qual deveria ser n para que a soma parcial

s n = ∑ i = 1 n 1 i + 1 satisfaça s n > 1000 ?

Passo 1

Eae gente tudo certo?! Bora resolver uma questãozinha de método integral.

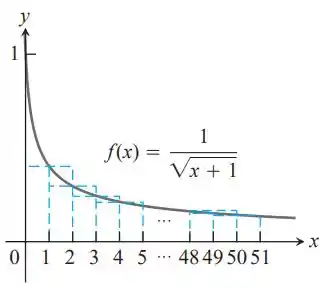
  1. Ambas as integrais podem representar a área debaixo da curva f x = 1 x + 1 e a soma s 50 pode ser considerada uma aproximação de cada integral utilizando o comprimento dos retângulos com x = 1 .

    2. A soma s 50 representa uma soma a esquerda, isto é, estamos escolhendo o ponto final a esquerda de cada subintervalos e devido a função ser decrescente, o valor de f é máximo nos pontos a esquerda de cada subintervalo.

    Dessa maneira, ∫ 1 51 1 x + 1 d x é menor do que s 50 , pois a área de cada retângulo é maior do que a área real.

    Passo 2

    Do mesmo modo para ∫ 0 50 1 x + 1 d x , pois s 50 representa a soma a direita de cada subintervalo, portanto ∫ 0 50 1 x + 1 d x é maior do que s 50 , pois o ponto final a direita de cada subintervalo é o ponto mínimo visto que a função é decrescente.

    Passo 3

    E finalmente, calculando as funções a partir de softwares matemáticos, ou é só aplicar uma substituição simples de x + 1 = u , temos que:

    ∫ 1 51 1 x + 1 d x < s 50 < ∫ 0 50 1 x + 1 d x

    2 x + 1 1 51 < s 50 < 2 x + 1 0 5 0

    11,6 < s 50 < 12,3

    Passo 4

  2. Essa é mais tranquilona, é só uma inequaçãozinha que iremos tirar de letra, vem comigo!

s n > 1000

∫ 1 n + 1 1 x + 1 d x > 1000

Substituindo x + 1 = u

∫ 1 u d u > 1000

2 x + 1 1 n + 1 > 1000

2 n + 1 - 2 2 > 1000

n + 1 2 > 1000 - 2 2 2 2

n > 251414,2

n ≥ 251415

Resposta

  1. Demonstração
  2. n ≥ 251415

Exercícios de Livros Relacionados

Nos Exercícios 17-44, utilize qualquer método para determinar se a série converge ou diverge. Justifique suas respostas. ∑ n = 1 ∞ 1 - 3 n n
Nos Exercícios 17-44, utilize qualquer método para determinar se a série converge ou diverge. Justifique suas respostas. ∑ n = 1 ∞ 1 n - 1 n 2 n
Nos Exercícios 17-44, utilize qualquer método para determinar se a série converge ou diverge. Justifique suas respostas. ∑ n = 1 ∞ 1 - 1 3 n n
Nos Exercícios 17-44, utilize qualquer método para determinar se a série converge ou diverge. Justifique suas respostas. ∑ n = 1 ∞ ln ⁡ n n 3
Nos Exercícios 17-44, utilize qualquer método para determinar se a série converge ou diverge. Justifique suas respostas. ∑ n = 1 ∞ 1 n - 1 n 2 n