Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.3 - Ex. 48
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.
Passo 1
Olá galerinha, vamos relembrar rapidinho a relação entre as coordenadas polares e cartesianas.
Quando utilizamos coordenadas polares e cartesianas em um plano, posicionamos as duas origens juntas e tomamos o raio polar inicial como o eixo positivo. O raio , , torna-se o eixo positivo. Os dois sistemas de coordenadas estão relacionados.
As seguintes equações determinam unicamente as coordenadas cartesianas e , dadas as coordenadas polares e :
Porém, se e são dadas, usamos as equações:
Passo 2
Sendo assim, do enunciado, temos a seguinte equação polar:
Para estabelecermos a relação entre as coordenadas polares e cartesianas, iremos multiplicar ambos os lados por :
Sendo assim:
Para completar o quadrado, faremos o seguinte:
E temos o seguinte gráfico:
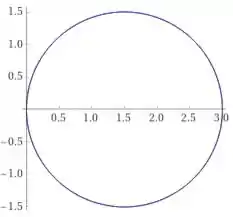
O gráfico é uma circunferência, , com raio .
Tchau pessoal, te espero em mais exercícios.
Resposta
, circunferência, , raio .