Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.4 - Ex. 54

A substituição trigonométrica x = a cos ⁡ θ poderia ser usada com uma integral cujo integrando envolva a 2 - x 2 . Determine uma restrição apropriada para θ com a substituição x = a cos ⁡ θ e discuta como aplicar essa substituição em integrais apropriadas. Ilustre sua discussão calculando a integral do Exemplo 1 usando uma substituição desse tipo.

Passo 1

Podemos usar a substituição trigonométrica x = a cos ⁡ θ para integrais envolvendo a 2 - x 2 com uma certa restrição para θ , vamos achar essa restrição.

Depois de utilizar essa substituição a expressão fica da seguinte forma:

a 2 - x 2 = a 2 - a 2 cos 2 ⁡ θ = a 2 1 - cos 2 ⁡ θ = a 1 - cos 2 ⁡ θ = a sen 2 ⁡ θ = a sen ⁡ θ

Agora para se livrar desse módulo nós queremos um θ onde sen ⁡ θ seja positivo, e isso acontece quando 0 ≤ θ ≤ π , assim achamos a restrição de θ para usar a substituição x = a cos ⁡ θ .

Passo 2

Agora vamos fazer a integral do exemplo 1 :

∫ d x x 2 4 - x 2

Usando a substituição pedida:

x = 2 cos ⁡ θ

d x = - 2 sen ⁡ θ d θ

Substituindo na integral vamos ficar com:

∫ d x x 2 4 - x 2 = ∫ - 2 sen ⁡ θ d θ 2 cos ⁡ θ 2 4 - 2 cos ⁡ θ 2 = ∫ - 2 sen ⁡ θ d θ 2 cos ⁡ θ 2 4 - 2 cos ⁡ θ 2 =

= ∫ - 2 sen ⁡ θ d θ 4 cos 2 ⁡ θ 4 - 4 cos 2 ⁡ θ = ∫ - 2 sen ⁡ θ d θ 4 cos 2 ⁡ θ 4 1 - cos 2 ⁡ θ

Agora vamos usar a identidade sen 2 ⁡ θ + cos 2 ⁡ θ = 1 :

∫ d x x 2 4 - x 2 = ∫ - 2 sen ⁡ θ d θ 4 cos 2 ⁡ θ 4 1 - cos 2 ⁡ θ = ∫ - sen ⁡ θ d θ 2 cos 2 ⁡ θ 4 sen 2 ⁡ θ = ∫ - sen ⁡ θ d θ 2 cos 2 ⁡ θ 2 sen ⁡ θ =

= ∫ - d θ 4 cos 2 ⁡ θ = - 1 4 ∫ d θ cos 2 ⁡ θ = - 1 4 ∫ sec 2 ⁡ θ d θ

Passo 3

Aqui, para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:

∫ sec 2 ⁡ x d x = tg ⁡ x + C

Aplicando:

∫ d x x 2 4 - x 2 = - 1 4 ∫ sec 2 ⁡ θ d θ = - 1 4 tg ⁡ θ + C

Agora vamos voltar a variável original x , precisamos saber tg ⁡ θ , vamos ver pela figura abaixo:

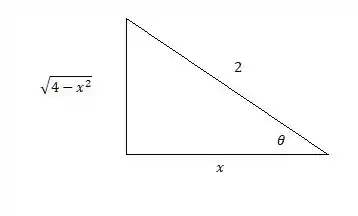
Temos então que:

tg ⁡ θ = 4 - x 2 x

Agora é só substituir e pronto:

∫ d x x 2 4 - x 2 = - 1 4 tg ⁡ θ + C = - 1 4 ⋅ 4 - x 2 x + C = - 4 - x 2 4 x + C

Resposta

0 ≤ θ ≤ π e ∫ d x x 2 4 - x 2 = - 4 - x 2 4 x + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral indefinida:int (sqrt(1 + x^2) + 2 x) d x
Calcule a integral indefinida:int sqrt(x^2 - 4) d x
Verifique se a integral imprópria converge. Em caso positivo, determine seu valor. ∫ 3 + ∞ d x x 2 - 4
Calcule a integral indefinida:int ((6 x + 5))/(sqrt(9 x^2 + 1)) d x
Calcule a integral indefinida:int (sen x + (x^2)/(sqrt(1 + x^2))) d x