Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 7
Suponha que a água de um tanque esteja sendo drenada por um orifício circular de área localizado no fundo do tanque. Foi mostrado experimentalmente que, quando o atrito da água no orifício é levado em consideração, o volume de água que sai do tanque por segundo é aproximadamente . Encontre a equação diferencial para a altura de água em qualquer instante no tanque cúbico da Figura 1.19. O raio do orifício mede
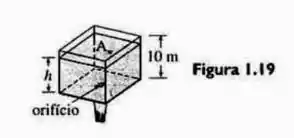
Passo 1
Olá, tudo bem?
Bom, considerando os dados do problema, podemos montar nossa equação diferencial como:
Usando e , temos:
E prontinho! Essa é a equação diferencial procurada 😉
Resposta
Exercícios de Livros Relacionados
a. Identifique os valores de equilíbrio. Quais são estáveis e quais são instáveis?b. Construa uma reta de fase. Identifique os sinais de y' e y".c. Esboce uma seleção representativa de curvas integrai
a. Identifique os valores de equilíbrio. Quais são estáveis e quais são instáveis?b. Construa uma reta de fase. Identifique os sinais de y' e y".c. Esboce uma seleção representativa de curvas integrai
Considere um tanque de água cilindro de seção reta constante A . Água é bombeada para o tanque a uma taxa constante k e sai através de um pequeno furo de área a no fundo do tanque. Do principio de Tor
Um lago é formado quando a água se acumula em uma depressão cônica de raio a e profundidade h . Suponha que a água flui para dentro a uma taxa constante k e é perdida por evaporação a uma taxa proporc
Considere a equação d y / d t= f ( y ) e suponha que y 1 é um ponto crítico, ou seja, f y 1 = 0 . Mostre que a solução de equilíbrio ϕ t = y 1 é assintoticamente estável se f ' y 10 e é assintoticamen