Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.2 - Ex. 8
8) Suponha P e Q de classe C1 em Ω = ℝ2 - {(0, 0), (1, 1)}. Suponha, ainda,
Calcule
Sabendo que
e
(γ1 e γ2 são orientadas no sentido horário e γ no sentido anti-horário.)
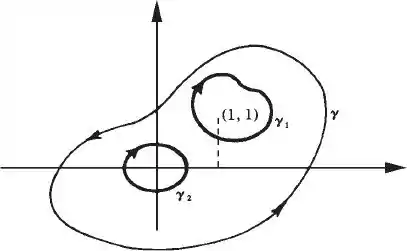
Passo 1
Essa questão é puramente Manipulação do TEOREMA DE GREEN que diz
Contudo temos duas regiões dentro do nosso conjunto total que estão sendo excluídas, logo podemos reescrever nosso teorema como
Nos estamos somando porque estão com rotação inversa de e isso é muito importante !!!! (Rotação anti-horário significa incluindo a região interior. Rotação Horaria significa excluindo a região interior )
Passo 2
Contudo o enunciado nos diz que
e
Passo 3
Então aquela conta enorme se resume a
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Exercícios de Livros Relacionados
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.h. ∮ C 2 x - y d x + x + 3 y d y C é a fronteira do pentágono de vértices 0,0 , 0,2 , 1,3 , 2,2 , 2,0
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.g. ∮ C 2 x - y 3 d x + - x y d y C é a fronteira da região limitada pelas curvas x 2 + y 2 = 4 x 2 + y 2 = 9
a) Mostre que a área de uma região fechada e limitada D do plano x y pode ser obtida através da seguinte integral de linha á r e aD = ∮ ∂ D xd y á
Seja F x , y = - y x 2 + y 2 , x x 2 + y 2 + 3 x um campo vetorial em R 2 . Calcule a integral de linha do campo F ao longo das curvas C 1 e C 2 , orientadas no sentido anti-horário, onde: C 1 é a cir
Seja F = F 1 , F 2 um campo vetorial de classe C 1 no R 2 exceto em 0,0 , tal que ∂ F 2 ∂ x x , y = ∂ F 1 ∂ y x , y + 4 para todo x , y ≠ 0,0 . Sabendo que ∮ γ F 1d x + F 2d y = 6 π , onde γ é a circu