Seja um campo vetorial de classe no exceto em , tal que para todo . Sabendo que , onde é a circunferência , orientada no sentido anti-horário, calcule , onde é a elipse orientada no sentido anti-horário.
Passo 1
Esse exercício parece ser ótimo caso para usarmos o teorema de Green, né?! Pois poderíamos fazer
e sabemos que . Assim...
e a última integral é simplesmente a área da elipse de semieixos , que é simplesmente dada por . Assim,
:D pareceu até que fácil, né?
A notícia ruim vem agora... o que fizemos acima está errado! Sim, levaríamos um baita de um zero numa prova. Mas por qual motivo que a resolução está errada?
O erro ocorreu por a gente aplicar o teorema de Green “cegamente”, sem olhar as condições impostas pelo teorema. Como está no interior de , e como não é de classe em , segue que não podemos aplicar o teorema de Green. :(
Porém, podemos fazer um truque! Veja a figura abaixo:
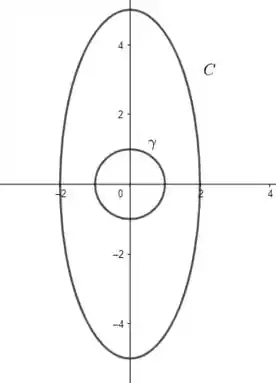
Se considerarmos nossa região como sendo o interior da elipse, menos a circunferência então poderemos aplicar o teorema de Green normalmente, pois não irá mais pertencer a .
Passo 2
Vamos fazer isso. Porém, devemos tomar cuidado que ao fazer isso não estamos mais calculando nossa integral original, mas sim a integral abaixo:
Agora, note que (pois devemos percorrer a curva no sentido oposto). Além disso,
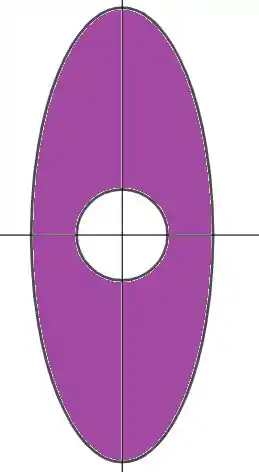
Sendo assim, temos
Resposta
.