Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.6 - Ex. 17

Suponha que as condições são como nos Problemas 15 e 16, exceto que a condição de contorno em x = 0 é u(0, t) = 40.

  1. Encontre a temperatura u(x, t).
  2. Faça o gráfico de u em função de x para diversos valores de t. Faça, também, o gráfico de u em função de t para diversos valores de x.
  3. Compare os gráficos obtidos nesse problema com os do Problema 16. Explique como a mudança na condição de contorno em x = 0 causa as diferenças observadas no comportamento da temperatura na barra.

Passo 1

A solução é dada pelo problema anterior:

u ( x , t ) = ∑ n = 1 ∞ c n e - ( 2 n - 1 ) ² π ² α ² t 4 L ² s e n [ ( 2 n - 1 ) π x 2 L ]

c n = 2 L ∫ 0 L f ( x ) s e n [ ( 2 n - 1 ) π x 2 L ] d x

Passo 2

Queremos achar c n :

c n = 40 ( 2 n - 1 ) ² π ² [ 6 c o s ( n π ) - ( 2 n - 1 ) π ]

Substituímos e achamos:

u ( x , t ) = 40 + ∑ n = 1 ∞ 40 ( 2 n - 1 ) 2 π 2 [ 6 c o s ( n π ) - ( 2 n - 1 ) π ] e - ( 2 n - 1 ) 2 π ² t 3600 s e n ( ( 2 n - 1 ) π x 60 )

Passo 3

Na letra b:

u versus t para x=5,15,25:

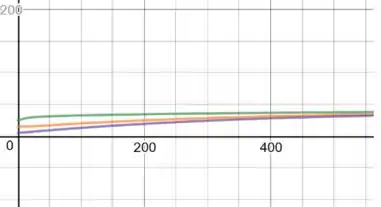
u versus x, para t=10,20,35:

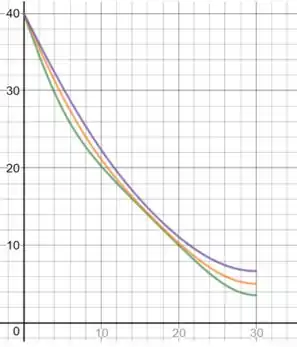
Passo 4

Na letra c:

O gráfico de u versus x é diferente do 16 pois agora começa em 40 e decresce ao invés de crescer e decrescer.

O gráfico u versus t agora se aproxima do valor estacionário 40 ao invés de 0.

Resposta

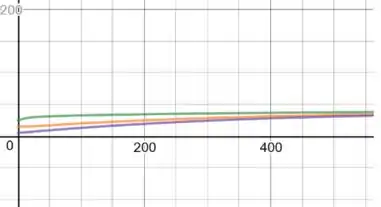
  1. u ( x , t ) = 40 + ∑ n = 1 ∞ 40 ( 2 n - 1 ) 2 π 2 [ 6 c o s ( n π ) - ( 2 n - 1 ) π ] e - ( 2 n - 1 ) 2 π ² t 3600 s e n ( ( 2 n - 1 ) π x 60 )

  3. O gráfico de u versus x é diferente do 16 pois agora começa em 40 e decresce ao invés de crescer e decrescer.

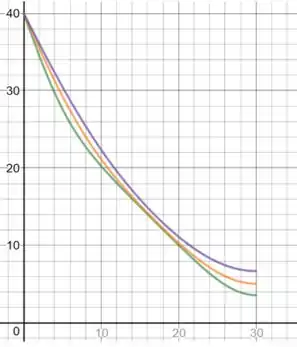
O gráfico u versus t agora se aproxima do valor estacionário 40 ao invés de 0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma barra uniforme de comprimento L a uma temperatura inicial dada por u ( x , 0 ) = s i n ( π x / L ) ,0 ≤ x ≤ L . Suponha que ambas as extremidades estão isoladas.Encontre a temperatura u(
Em cada um dos problemas de 1 a 8, encontre a solução estado estacionário da equação do calor α 2 u x x = u t que satisfaz o conjunto dado de condições de contorno. u x ( 0 , t ) = 0 ,u ( L , t ) = T
Em cada um dos problemas de 1 a 8, encontre a solução estado estacionário da equação do calor α 2 u x x = u t que satisfaz o conjunto dado de condições de contorno. u ( 0 , t ) = T ,u x ( L , t ) = 0
Considere uma barra com 30 cm de comprimento para a qual α 2 = 1 . Suponha que a distribuição inicial de temperatura é dada por u(x, 0) = x(60 – x)/30 e que as condições de contorno são u(0, t) = 30 e
Em cada um dos problemas de 1 a 8, encontre a solução estado estacionário da equação do calor α 2 u x x = u t que satisfaz o conjunto dado de condições de contorno. u ( 0 , t ) = 0 ,u ( L , t ) = 0