Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.6 - Ex. 12

Considere uma barra uniforme de comprimento L a uma temperatura inicial dada por u ( x , 0 ) = s i n ( π x / L ) ,   0 ≤ x ≤ L . Suponha que ambas as extremidades estão isoladas.

  1. Encontre a temperatura u(x, t).
  2. Qual é a temperatura no estado estacionário, quando t → ∞ ?
  3. Sejam α 2 = 1 e L = 40 . Faça o gráfico de u em função de x para diversos valores de t. Faça, também, o gráfico de u em função de t para diversos valores de x.
  4. Descreva em poucas palavras como a temperatura na barra varia com o passar do tempo.

Passo 1

Temos:

u ( x , 0 ) = s e n ( π x L ) ,   0   ≤   x   ≤   L

E a solução é dada pelas fórmulas 35 e 37 na página 637:

u ( x , t ) = c 0 2 + ∑ n = 1 ∞ c n e - n ² π ² α ² t L ² c o s ( n π x L )

c n = 2 L ∫ 0 L f ( x ) c o s ( n π x L )

Passo 2

Temos:

c 0 = 2 L ∫ 0 L s e n ( π x L ) d x = 4 π

e queremos achar c n :

c n = 0 ,   n   é   í m p a r

- 4 ( n ² - 1 ) π ,   n   é   p a r

Substituímos e achamos:

u ( x , t ) = 2 π + ∑ n = 1 ∞ c n e - n ² π ² α ² t L ² c o s ( n π x L )  

Passo 3

Na letra b:

t ⇒ ∞ ,   e - n ² π ² α ² t L ² ⇒ 0 , então a temperatura em estado permanente é 2 π

Passo 4

Na letra c:

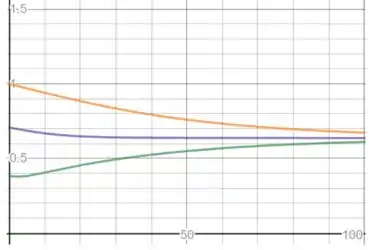
u versus t para x=5,20,30:

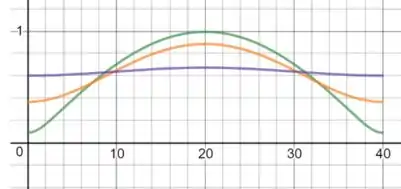
u versus x, para t=1,20,100:

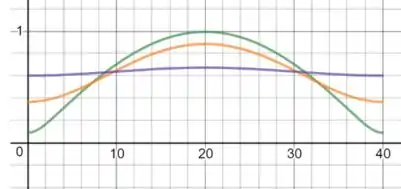
Passo 5

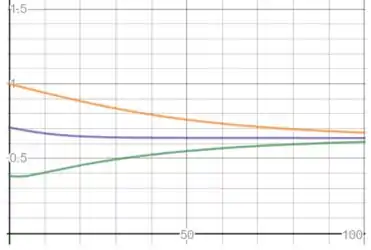
Na letra d:

Podemos ver que a solução começa como um seno e suaviza até o estado permanente, que é a constante 2 π

Resposta

  1. u ( x , t ) = 2 π + ∑ n = 1 ∞ c n e - n ² π ² α ² t L ² c o s ( n π x L )  
  2. t ⇒ ∞ ,   e - n ² π ² α ² t L ² ⇒ 0 , então a temperatura em estado permanente é 2 π

  4. Podemos ver que a solução começa como um seno e suaviza até o estado permanente, que é a constante 2 π
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja L um operador diferencial de segunda ordem. Mostre que a solução y = ϕ x do problema L y = f x , α 1 y 0 + α 2 y ' 0 = a ,β 1 y 1 + β 2 y ' 1 = b pode ser escrita como y = u + v , onde u = ϕ 1 x
Considere o problema y ' ' + p x y ' + q x y = 0 ,y 0 = a ,y 1 = b . Suponha que y = u + v , em que v é qualquer função duas vezes diferenciável satisfazendo as condições de contorno (mas não necessar
Nos problemas de 1 a 5, resolva o problema dado usando expansões em autofunções.4. y ' ' + 2 y ' = - x ,y ' 0 = 0 ,y ' 1 + y 1 = 0 ; Veja seção 11.2, Problema 11.
Nos problemas de 10 a 13, determine se existe algum valor da constante a para o qual o problema tem solução. Encontre a solução para cada um desses valores.13. y ' ' + π 2 y = a - c o s π x ,y 0 = 0 ,
Em cada problema de 19 a 22, use a expansão em autofunções para encontrar a solução do problema de contorno dado.20. u t = u x x + e - t ,u x 0 , t = 0 ,u x 1 , t + u 1 , t = 0 ,u x ,0 = 1 - x ; Veja