Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 67

Suponha que f x = ( x 2 - 9 ) / ( x + 3 )

  1. Crie uma tabela de valores de f nos pontos x = - 3,1 ;   - 3,01 ;   - 3,001 e assim por diante, até onde sua calculadora permita. Em seguida estime lim x → - 3 ⁡ f ( x ) . A que estimativa você chega se, em vez disso, avaliar f em x = - 2,9 ;   - 2,99 ;   - 2,999
  2. Apoie suas conclusões no item a fazendo o gráfico de f próximo a x 0 = - 3 e utilizando os comandos Zoom e Trace para estimar os valores de y no gráfico quando x → - 3  
  3. Determine lim x → - 3 ⁡ f ( x ) algebricamente como no exemplo 7.

Passo 1

Na letra (a) não tem muito o que fazer, precisamos criar essas tabelas. Uma para valores menores que x = - 3 e outra para valores maiores (vou usar 5 pontos na tabela)

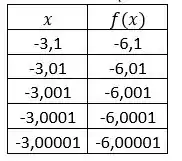
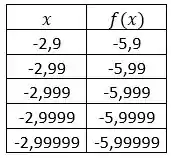
Pelas tabelas estamos vendo que a função se aproxima cada vez mais de - 6 , então podemos concluir que

lim x → - 3 ⁡ f ( x ) = - 6

Passo 2

b) O esboço dessa função é esse aqui:

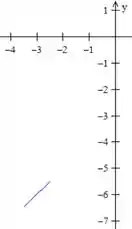
Realmente observamos que a função se aproxima de - 6 ao nos aproximarmos de 3

Passo 3

c) Como temos um polinômio do segundo grau no numerador a boa é fatorar essa expressão.

Nesse caso, vamos usar a diferença de quadrados que diz

a 2 - b 2 = ( a - b ) ( a + b )

No nosso caso a = x e b = 3 , então

x 2 - 9 = ( x + 3 ) ( x - 3 )

Passo 4

Então vamos ter o seguinte

lim x → - 3 ⁡ x 2 - 9 x + 3 = lim x → - 3 ⁡ ( x - 3 ) ( x + 3 ) x + 3 lim x → - 3 ⁡ x - 3

Substituindo o valor temos que

lim x → - 3 ⁡ x 2 - 9 x + 3 = - 6

Resposta

a)

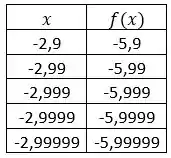
b)

c) lim x → - 3 ⁡ x 2 - 9 x + 3 = - 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a função g x representada graficamente aqui, determine os seguintes limites ou explique por que eles não existem a ) lim x → 1 ⁡ g x b ) lim x → 2 ⁡ g x c ) lim x → 3 ⁡ g x d ) lim x → 2,5 ⁡ g x
Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma lim h → 0 ⁡ f x + h - f ( x ) h Ocorrem com frequência em cálculo. Nos exercícios 57-62, avalie esse limite p
Suponha que lim x → b ⁡ f ( x ) = 7 e lim x → b ⁡ g ( x ) = - 3 . Determine lim x → b ⁡ g x + f ( x ) lim x → b ⁡ g ( x ) f x lim x → b ⁡ 4 g ( x ) lim x → b ⁡ f x g x
Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma lim h → 0 ⁡ f x + h - f ( x ) h Ocorrem com frequência em cálculo. Nos exercícios 57-62, avalie esse limite p
Suponha que lim x → 1 ⁡ h ( x ) = 5 , lim x → 1 ⁡ p ( x ) = 1 e lim x → 1 ⁡ r ( x ) = 2 . Especifique quais regras do teorema 1 são utilizadas para efetuar as etapas a , b , c do cálculo a seguir lim