Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 66

  1. Suponha que as desigualdades

    2. 1 2 - x 2 24 < 1 - cos ⁡ x x 2 < 1 2

    Valham para valores de x próximos a zero (e elas valem como você verá na seção 10.9). O que dizer a respeito de

    lim x → 0 ⁡ 1 - cos ⁡ x x 2

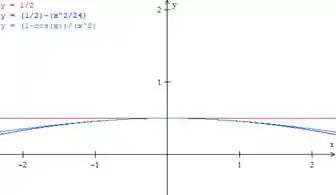
  2. Faça os gráficos das equações y = 1 2 - x 2 24 , y = 1 - cos ⁡ x x 2 e y = 1 2 juntas para - 2 ≤ x ≤ 2 .

Comente o comportamento dos gráficos quando x → 0 .

Passo 1

Nessas questões em que ele fala que a sua função está limitada por outras duas a boa é usar o teorema do confronto ou do sanduiche para os íntimos!

Passo 2

Legal, mas quais as funções dos extremos? Ele mesmo já deu g x = 1 2 - x 2 24 e h x = 1 2 .

Então pelo teorema, vamos ter que

lim x → 0 ⁡ g ( x ) ≤ lim x → 0 ⁡ 1 - cos ⁡ x x 2 ≤ lim x → 0 ⁡ h ( x )

lim x → 0 ⁡ 1 2 - x 2 24 ≤ lim x → 0 ⁡ 1 - cos ⁡ x x 2 ≤ lim x → 0 ⁡ 1 2

Passo 3

Agora precisamos determinar o valor dos limites das pontas. Vamos começar com o da esquerda e lembre sempre que a primeira coisa a fazer com limites e substituir o valor do ponto:

lim x → 0 ⁡ 1 2 - x 2 24 = 1 2 - 0 2 24 = 1 2

Agora o da direita

lim x → 0 ⁡ 1 2 = 1 2

Passo 4

Agora para uma coisa ser ao mesmo tempo maior ou igual a 1 2 e menor ou igual a 1 2 , ela tem que ser na verdade igual a 1 2 (essa é a lógica do teorema do confronto).

Logo,

lim x → 0 ⁡ 1 - cos ⁡ x x 2 = 1 2

Passo 5

Esboçando os gráficos como ele pediu, vamos ter

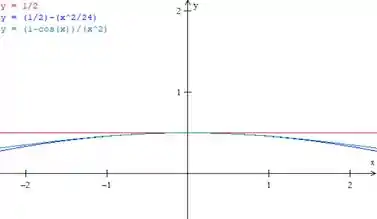
Vejam como a função em verde está sempre entre as outras duas nesse intervalo!

Além disso, olha como, ao se aproximar de 0 , a função de azul vai se aproximando da vermelha e levando a verde junto. Essa é a ideia do teorema do confronto!

Resposta

a ) 1 2

b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam a , b e c reais fixos e suponha que, para todo x , a + b x + c x 2 ≤ x 3 . Prove que a = b = c = 0 .
Calcule, caso existe, lim x → 0 ⁡ f x - f 0 x - 0 em que f é dada por f x = x 2 sen ⁡ 1 x s e x ≠ 0 0 s e x = 0
Seja f uma função definida em R tal que para todo x ≠ 1 , - x 2 + 3 x ≤ f xx 2 - 1 x - 1 . Calcule lim x → 1 ⁡ f x e justifique.
Verifique que lim x → 0 ⁡ sen ⁡ 1 x não existe.Calcule, caso exista, lim x → 0 ⁡ x sen ⁡ 1 x . (Justifique)
Seja f definida em R e suponha que exista M0 tal que, para todo x , f x - f p ≤ M x - p 2 .Mostre que f é contínua em p .Calcule, caso exista, lim x → p ⁡ f x - f p x - p .