Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.6 - Ex. 4
- Verifique que não existe.
- Calcule, caso exista, . (Justifique)
Passo 1
Fala, galera! Tudo bem? Vamos resolver essa questão!
O enunciado pediu pra gente verificar que o limite da função quando tende a zero não existe e calcular o limite de .
Nos dois casos vamos usar o Teorema do confronto para nos ajudar. Sabemos que a função seno é limitada entre e , para qualquer argumento na função. Então, temos:
E o teorema do confronto nos diz que quando temos uma função limitada assim, o limite das extremidades tem o mesmo valor, então o limite da função do meio também será igual.
Vamos usar isso como base para verificar a existência o primeiro limite e calcular o segundo.
Vamos lá!
Passo 2
Nós vimos no passo que:
Então, aplicando o limite, vamos ter:
O limite da constante é a própria constante, assim temos:
Repare que o que acontece é que a função fica oscilando entre e quando vai se aproximando de zero. A gente pode ver isso melhor no gráfico:
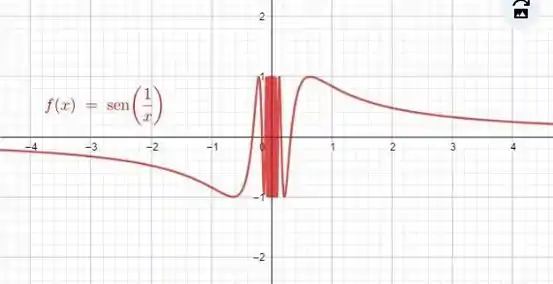
Passo 3
Agora para calcular vamos usar a mesma relação do passo :
Multiplicando todo mundo por , temos:
E aplicando o limite para :
Então, quando tende a zero, vamos ter:
E pelo Teorema do Confronto, podemos dizer que:
Valeu, galera! Até a próxima! 😉
Resposta
a)
b)