Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 64
63-66. Suponha que a água esteja fluindo a uma taxa constante para dentro dos frascos mostrados. Faça um esboço grosseiro do gráfico do nível de água versus tempo . Assegure-se de que o esboço mostre onde o gráfico é côncavo para baixo e para cima e destaque as coordenadas dos pontos de inflexão.
Passo 1
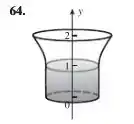
Então pessoal, considerando que alguém esteja enchendo o frasco em questão a uma taxa constante, para esboçarmos de maneira muito grosseira o gráfico de (nível de água) em função do tempo , precisamos levar em consideração apenas uma coisa: o formato do frasco! Note que o frasco que nos foi dado possui duas variações, se liga:
De até o frasco mantém sua largura;
De até o frasco vai aumentando sua largura.
Tudo bem, mas o que essas informações querem dizer? O tempo necessário para encher o frasco de até é menor do que o tempo necessário para encher o frasco de até , uma vez que a primeira parte é mais”fina”, como já dito!
Passo 2
Beleza, tendo em vista as informações do passo 1, se esboçarmos o gráfico teremos algo assim:
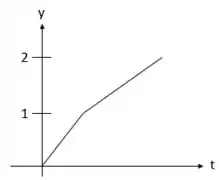
Vale ressaltar que, de acordo com o esboço, o gráfico não possui concavidades e muito menos pontos de inflexão, então não temos pontos especiais para apontar!
E está aí nossa resolução, galera!
Resposta
O gráfico não possui concavidade e nem ponto de inflexão.