- Suponha que as extremidades de uma barra de cobre com 100 cm de comprimento são mantidas a 0°C. Suponha que o centro da barra é aquecido a 100°C por uma fonte externa de calor; que essa situação se mantém até resultar em um estado estacionário. Encontre essa distribuição de temperatura no estado estacionário.
- Em um instante t = 0 [depois de atingido o estado estacionário do item (a)], suponha que a fonte externa é removida. No mesmo instante, suponha que a extremidade x = 0 é colocada em contato com um reservatório a 20°C, enquanto a outra extremidade permanece a 0°C. Encontre a temperatura em função da posição e do tempo.
- Faça o gráfico de u em função de x para diversos valores de t. Faça, também, o gráfico de u em função de t para diversos valores de x.
- A que valor limite tende a temperatura no centro da barra depois de um longo período de tempo? Depois de quanto tempo o centro da barra esfriará de modo a ficar a 1°C de seu valor limite?
Passo 1
Letra a:
Temos as seguintes condições:
Para encontrar a distribuição constante de temperatura, podemos dividir o problema em dois problemas. Sabemos que o centro da barra é aquecido a 100ºC. Então nós temos:
e
Passo 2
A distribuição constante de temperatura para esses problemas é dada por
Para o primeiro problema que temos , temos:
Para o segundo problema, temos . No entanto, observe que x começa em 50. Portanto, devemos escrever x-50 ao invés de x para começar em zero, para que tenhamos:
Combinando esses dois problemas, podemos escrever a distribuição constante de temperatura do nosso problema como:
Passo 3
Na letra b:
Agora, nosso problema é:
A solução do problema é dado pelas fórmulas 16 e 17 na página 634:
Passo 4
Nós temos e
Queremos achar :
Substituímos e chegamos em:
Passo 5
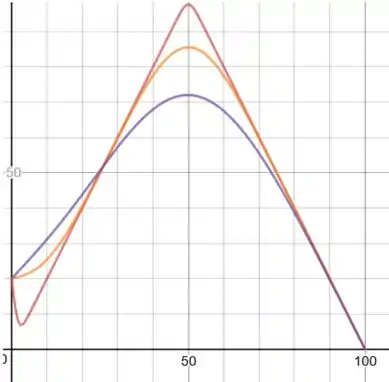
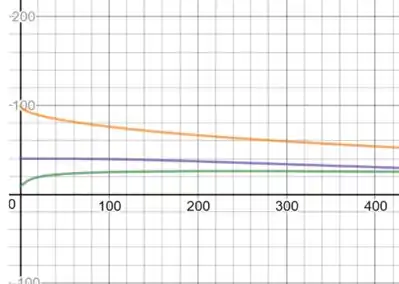
Na letra c:
u versus t, para x=5, x=50, x=80:
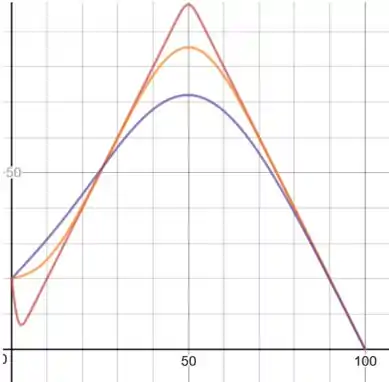
Passo 6
u versus x, para t=1, t=36, t=136
Passo 7
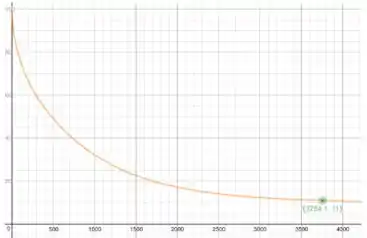
Na letra d:
Como , concluímos que a temperatura no centro se aproxima de
Quando a temperatura é 11ºC, o tempo é 3754.1:
Resposta
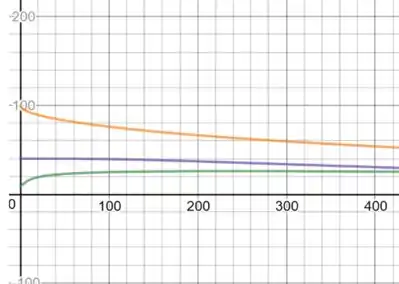
- 3754.1