Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.3 - Ex. 7

Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.

f x = x , - π ≤ x < 0 , 0 , 0 ≤ x < π

f x + 2 π = f ( x )

(a) Encontre a série de Fourier da função dada.

(b) Seja e n x = f x - s n ( x ) . Encontre a menor cota superior ou o valor máximo (se existir) de e n ( x ) para n = 10, 20 e 40.

(c) Se possível, encontre o menor n para o qual e n ( x ) ≤ 0,01 para todo x .

Passo 1

O item (a) nos pede para encontrar a série de Fourier para a função periódica:

f x = x , - π ≤ x < 0 , 0 , 0 ≤ x < π

A série de Fourier é uma equação da forma:

f x = a 0 2 + ∑ n = 1 m a n cos ⁡ n π x L + b n sen ⁡ n π x L

Em que a 0 , a n e b n são constantes definidas para cada valor de n = 1 ,   2 ,   … ,   ∞ e, L corresponde ao intervalo original em que a função periódica é definida ( - L ≤ x < L ) .

Precisamos então obter os termos a 0 ,   a n ,   b n e L . O intervalo de uma função escrita como série de Fourier é definido como - L ≤ x < L . Então, para a nossa função L = π . Tudo bem?

O próximo passo é o cálculo dos coeficientes. O coeficiente a 0 é definido por:

a 0 = 1 L ∫ - L L f x d x

Substituindo a função f ( x ) :

a 0 = 1 π ∫ - π 0 x d x + ∫ 0 π 0 d x

a 0 = 1 π ∫ - π 0 x d x

a 0 = 1 π x 2 2 - π 0

a 0 = 1 π 0 - π 2 2

a 0 = - π 2

Agora vamos determinar a n . Ele é dado por:

a n = 1 L ∫ - L L f x cos ⁡ n π x L d x

Aplicando f ( x ) e L ficamos com

a n = 1 π ∫ - π 0 x cos ⁡ n π x π d x + ∫ 0 π 0 cos ⁡ n π x π d x

a n = 1 π ∫ - π 0 x cos ⁡ n x d x

a n = 1 π 1 n x sen ⁡ n x - π 0 - 1 n ∫ - π 0 sen ⁡ n x d x

a n = 1 π 1 n 0 - - π sen ⁡ - n π + 1 n 2 cos ⁡ n x - π 0

Como n é um inteiro, sen ⁡ n π = 0 , para qualquer valor de n . Então:

a n = 1 π 1 n 0 - 0 + 1 n 2 ( cos ⁡ 0 - cos ⁡ - n π )

a n = 1 π n 2 ( 1 - cos ⁡ n π )

Por fim, vamos calcular b n . Ele é dado por:

b n = 1 L ∫ - L L f x sen ⁡ n π x L d x

Substituindo f ( x ) e L :

b n = 1 π ∫ - π 0 x sen ⁡ n π x π d x + ∫ 0 π 0 sen ⁡ n π x π d x

b n = 1 π ∫ - π 0 x sen ⁡ n x d x

b n = 1 π - 1 n x cos ⁡ n x - π 0 + 1 n ∫ - π 0 cos ⁡ n x d x

b n = 1 π - 1 n 0 - - π cos ⁡ - n π + 1 n 2 sen ⁡ n x - π 0

b n = 1 π - 1 n ( π cos ⁡ n π ) + 1 n 2 sen ⁡ 0 - sen ⁡ - n π

b n = - 1 n ( cos ⁡ n π )

Aplicando na função:

f x = - π 2 2 + ∑ n = 1 m 1 π n 2 ( 1 - cos ⁡ n π ) cos ⁡ n π x π - 1 n ( cos ⁡ n π ) sen ⁡ n π x π

f x = - π 4 + ∑ n = 1 m 1 π n 2 1 - cos ⁡ n π cos ⁡ n x - 1 n ( cos ⁡ n π ) sen ⁡ n x

O termo 1 - cos ⁡ n π terá valor 0 para n par e valor 2 para os n ímpar. Tudo bem? Se não ficou claro, vamos usar o exemplo de n = 1 e n = 2 . Para n = 1 :

cos ⁡ π = - 1 → 1 - cos ⁡ n π = 2

Para n = 2 :

cos ⁡ 2 π = 1 → 1 - cos ⁡ n π = 0

Então, para o somatório da parte cosseno apenas os valores de n ímpar são relevantes. Para garantir que vamos somar apenas os termos ímpares vamos substituir n por 2 n - 1 e, 1 - cos ⁡ n π por 2. Tudo bem?

Então

f x = - π 4 + ∑ n = 1 m 1 π ( 2 n - 1 ) 2 2 cos ⁡ ( 2 n - 1 ) x - 1 n ( cos ⁡ n π ) sen ⁡ n x

Além disso, a função cos ⁡ n π tem valor - 1 para n ímpar e 1 para n par. Então, vamos reescrevê-la como:

cos ⁡ n π = - 1 n

Nossa série fica:

f x = - π 4 + 2 π ∑ n = 1 m cos ⁡ 2 n - 1 x 2 n - 1 2 + ∑ n = 1 m - 1 n + 1 n sen ⁡ n x

Passo 2

Vamos agora para o item (b). Ele nos pede para calcular a diferença entre o valor da função original f ( x ) e a série de Fourier, usando a soma de n = 10 ,   20 e 40 termos. Para fazer isso, iremos usar o Excel para calcular os coeficientes a n e b n e, para realizar o somatório da série de Fourier. Após encontrar os valores da série para x dentro do intervalo original, iremos verificar em qual ponto ocorre o erro máximo.

Para n = 10 : e m á x = e ( - π ) = 1,59

Para n = 20 : e m á x = e ( - π ) = 1,58

Para n = 40 : e m á x = e ( - π ) = 1,57

Passo 3

O item (c) nos pede para verificar se existe um número n de termos que assegurem e n ( x ) ≤ 0,01 para todos os pontos. Para isso, vamos continuar o raciocínio do item (b) e extender o somatório para um maior número de termos. Se olharmos mais de perto para os valores de e ( - π ) :

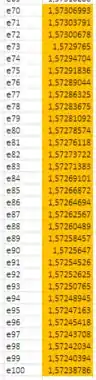
Podemos ver que o valor de e ( - π ) pouco se altera. Então, podemos concluir que não haverá um valor de n que assegure e n < 0,01 .

Resposta

(a) f x = - π 4 + 2 π ∑ n = 1 m cos ⁡ 2 n - 1 x 2 n - 1 2 + ∑ n = 1 m - 1 n + 1 n sen ⁡ n x .

(b) n = 10 : e m á x = e ( - π ) = 1,59

n = 20 : e m á x = e ( - π ) = 1,58

n = 40 : e m á x = e ( - π ) = 1,57

(c) Não existe n que assegure e n < 0,01 para todo x .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = 0 , - 1 ≤ x0 , x 2 , 0 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da fu
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x + 2 , - 2 ≤ x0 , 2 - 2 x , 0 ≤ x2 f x + 4 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) S
Encontre a solução formal do problema de valor inicial y ' ' + ω 2 y = f ( t ) , y 0 = 0 , y ' 0 = 0 Em que f é periódica com período 2 π e f t = 1 , 0tπ , 0 , t = 0 , π , 2 π , - 1 , πt2 π
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x - x 3 , - 1 ≤ x1 f x + 2 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) Seja e n x = f x -