Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.3 - Ex. 11

Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.

f x = 0 , - 1 ≤ x < 0 , x 2 , 0 ≤ x < 1

f x + 2 = f ( x )

(a) Encontre a série de Fourier da função dada.

(b) Seja e n x = f x - s n ( x ) . Encontre a menor cota superior ou o valor máximo (se existir) de e n ( x ) para n = 10, 20 e 40.

(c) Se possível, encontre o menor n para o qual e n ( x ) ≤ 0,01 para todo x .

Passo 1

O item (a) nos pede para encontrar a série de Fourier para a função periódica:

f x = 0 , - 1 ≤ x < 0 , x 2 , 0 ≤ x < 1

A série de Fourier é uma equação da forma:

f x = a 0 2 + ∑ n = 1 m a n cos ⁡ n π x L + b n sen ⁡ n π x L

Em que a 0 , a n e b n são constantes definidas para cada valor de n = 1 ,   2 ,   … ,   ∞ e, L corresponde ao intervalo original em que a função periódica é definida ( - L ≤ x < L ) .

Precisamos então obter os termos a 0 ,   a n ,   b n e L . O intervalo de uma função escrita como série de Fourier é definido como - L ≤ x < L . Então, para a nossa função L = 1 . Tudo bem?

O próximo passo é o cálculo dos coeficientes. O coeficiente a 0 é definido por:

a 0 = 1 L ∫ - L L f x d x

Substituindo a função f ( x ) :

a 0 = 1 1 ∫ - 1 0 0 d x + ∫ 0 1 x 2 d x

a 0 = ∫ 0 1 x 2 d x

a 0 = x 3 3 0 1

a 0 = 1 3 - 0

a 0 = 1 3

Agora vamos determinar a n . Ele é dado por:

a n = 1 L ∫ - L L f x cos ⁡ n π x L d x

Aplicando f ( x ) e L ficamos com

a n = 1 1 ∫ - 1 0 0 cos ⁡ n π x d x + ∫ 0 1 x 2 cos ⁡ n π x d x

a n = ∫ 0 1 x 2 cos ⁡ n π x d x

a n = 1 n π x 2 sen ⁡ n π x 0 1 - 2 n π ∫ 0 1 x sen ⁡ n π x d x

a n = 1 n π sen ⁡ n π - 0 - 2 n π - 1 n π x cos ⁡ n π x 0 1 + 1 n π ∫ 0 1 cos ⁡ n π x d x

Como n é um inteiro, sen ⁡ n π = 0 , para qualquer valor de n . Então:

a n = - 2 n π - 1 n π ( cos ⁡ n π ) + 1 n π 2 sen ⁡ n π x 0 1

a n = - 2 n π - 1 n π cos ⁡ n π + 1 n π 2 ( sen ⁡ n π - sen ⁡ 0 )

a n = 2 n π 2 cos ⁡ n π

Por fim, vamos calcular b n . Ele é dado por:

b n = 1 L ∫ - L L f x sen ⁡ n π x L d x

Substituindo f ( x ) e L :

b n = 1 1 ∫ - 1 0 0 sen ⁡ n π x d x + ∫ 0 1 x 2 sen ⁡ n π x d x

b n = ∫ 0 1 x 2 sen ⁡ n π x d x

b n = - 1 n π ( x 2 cos ⁡ n π x ) 0 1 + 2 n π ∫ 0 1 x cos ⁡ n π x d x

b n = - 1 n π cos ⁡ n π - 0 + 2 n π 1 n π x sen ⁡ n π x 0 1 - 1 n π ∫ 0 1 sen ⁡ n π x d x

b n = - 1 n π cos ⁡ n π + 2 n π 1 n π sen ⁡ n π x - 0 + 1 n π 2 cos ⁡ n π - cos ⁡ 0

b n = - 1 n π cos ⁡ n π + 2 n π 0 + 1 n π 2 cos ⁡ n π - 1

b n = - 1 n π cos ⁡ n π + 2 n π 3 ( cos ⁡ n π - 1 )

b n = - 2 n π 3 + 2 n π 3 - 1 n π cos ⁡ n π

Aplicando na função:

f x = ( 1 / 3 ) 2 + ∑ n = 1 m 2 n π 2 cos ⁡ n π cos ⁡ n π x + 2 n π 3 - 1 n π cos ⁡ n π - 2 n π 3 sen ⁡ n π x

Além disso, como a função cos ⁡ n π tem valor - 1 para n ímpar e 1 para n par, podemos reescrevê-la como:

cos ⁡ n π = - 1 n

Nossa série fica:

f x = 1 6 + 2 π 2 ∑ n = 1 m - 1 n n 2 cos ⁡ n π x + ∑ n = 1 m 2 n π 3 - 1 n π - 1 n - 2 n π 3 sen ⁡ n π x

Passo 2

Vamos agora para o item (b). Ele nos pede para calcular a diferença entre o valor da função original f ( x ) e a série de Fourier, usando a soma de n = 10 ,   20 e 40 termos. Para fazer isso, iremos usar o Excel para calcular os coeficientes a n e b n e, para realizar o somatório da série de Fourier. Após encontrar os valores da série para x dentro do intervalo original, iremos verificar em qual ponto ocorre o erro máximo.

Para n = 10 : e m á x = e ( 1 ) = 0,5193

Para n = 20 : e m á x = e ( 1 ) = 0,5099

Para n = 40 : e m á x = e ( 1 ) = 0,505

Passo 3

O item (c) nos pede para verificar se existe um número n de termos que assegurem e n ( x ) ≤ 0,01 para todos os pontos. Para isso, vamos continuar o raciocínio do item (b) e extender o somatório para um maior número de termos. Se olharmos mais de perto para os valores de e ( 1 ) :

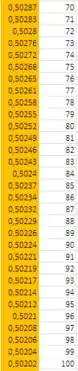
Podemos ver que o valor de e ( 1 ) pouco se altera. Então, podemos concluir que não haverá um valor de n que assegure e n < 0,01 .

Resposta

(a) f x = 1 6 + 2 π 2 ∑ n = 1 m - 1 n n 2 cos ⁡ n π x + ∑ n = 1 m 2 n π 3 - 1 n π - 1 n - 2 n π 3 sen ⁡ n π x .

(b) n = 10 : e m á x = e ( 1 ) = 0,5193

n = 20 : e m á x = e ( 1 ) = 0,5099

n = 40 : e m á x = e ( 1 ) = 0,505

(c) Não existe n que assegure e n < 0,01 para todo x .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Supondo que f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n π x L + b n sen ⁡ n π x L , Mostre, formalmente, que 1 L ∫ - L L f x 2 d x = a 0 2 2 + ∑ n = 1 ∞ ( a n 2 + b n 2 )
Encontre a solução do problema de valor inicial y ' ' + ω 2 y = sen ⁡ n t , y 0 = 0 , y ' 0 = 0 Em que n é um inteiro positivo e ω 2 ≠ n 2 . O que acontece se ω 2 = n 2 ?
Encontre a solução formal do problema de valor inicial y ' ' + ω 2 y = f ( t ) , y 0 = 0 , y ' 0 = 0 Em que f é periódica com período 2 π e f t = 1 , 0tπ , 0 , t = 0 , π , 2 π , - 1 , πt2 π
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x - x 3 , - 1 ≤ x1 f x + 2 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) Seja e n x = f x -
(a) Se f e f ' forem seccionalmente contínuas em - L → xL e se f for periódica com período 2 L , mostre que n a n e n b n permanecerão limitadas quando n → ∞ .(b) Se f for contínua em - L ≤ x ≤ L e pe