Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.4 - Ex. 86
Suponha que é uma função positiva. Se , mostra que
Isto mostra que não é uma forma indeterminada.
Passo 1
E aí meus amores nessa questãozinha “Pegue o que puder, sem nada a devolver” okay?
A questão nos pede para mostrar que, se temos uma função que tende a quando se aproxima de e uma função que tende ao infinito quando se aproxima de então a função tende a 0 quando se aproxima de
Isso demonstraria que a expressão não é uma forma indeterminada.
Para resolver isso, vamos usar a definição e propriedades dos limites, além das propriedades logarítmicas.
Nossa estratégia será transformar a expressão de modo que possamos aplicar os limites de forma mais clara.
A teoria que usaremos envolve a transformação logarítmica:
Transformação Logarítmica:
Se
Então podemos tomar o logaritmo natural dos dois lados:
Se liga também na resolução do solucionário, ela tá um pouco mais sólida:
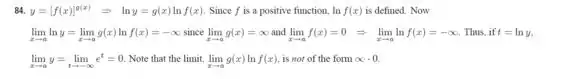
Mas cuidado oq essa resolução é muito pouco explicada, tem que colocar no “modelo RA”
Usando a propriedade dos logaritmos temos:
Precisamos estudar o limite de quando .
Dado que e isso sugere que precisamos examinar a forma indeterminada
Passo 2
Precisamos relacionar o que foi dado com o que está pedindo. Boraaaa....
Estamos dados que:
E
Queremos provar que:
Passo 3
Vamos seguir a estratégia que discutimos:
Transformação Logarítmica:
Estudo do Limite:
- Sabemos que implica
- Sabemos que
Assim, temos que estudar o comportamento de onde e
Produto de Infinitos:
Vamos examinar isso mais de perto usando o limite.
Passo 4
Vamos reescrever de modo que seja mais fácil manipular o limite.
Uma forma comum é usar substituições adequadas ou expandir em séries, mas, frequentemente, podemos diretamente examinar:
Observe que muito rapidamente, e cresce.
Vamos considerar uma aproximação comum:
Então, temos:
Passo 5
Lembre-se que implica que deve ser
Portanto:
Dessa forma, mostramos que
Confirmando que não é uma forma indeterminada.
Depois dessa questão, “Ninguém se mexe” Meu cérebro caiu.”
Haha bora pra proóximaaaa
Resposta
Vide a demonstração.