56. Suponha que e , onde é derivável em 3. Prove que
Passo 1
Como o enunciado não nos traz muitas informações, devemos utilizar do conceito de derivada de função composta, bem como encontrar, utilizando a regra da cadeia, quem é a função h’(x) uma vez que a mesma não nos foi fornecida.
Passo 2
Assim, utilizando a regra da cadeia temos que
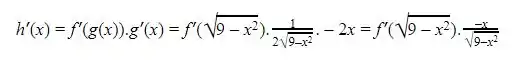
Passo 3
Substituindo x = 0 na equação acima , vem que
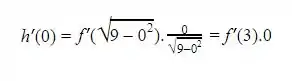
Como do enunciado ele diz que f ’(3) existe temos que
![]()
Resposta
Demonstração.