Dada (a) Faça um esboço do gráfico de f. (b) Ache , se existir. (c) Ache se existir
Passo 1
Para a letra (a), o gráfico ficará da seguinte forma:
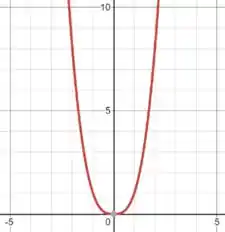
Passo 2
Na letra (b) precisaremos calcular o limite da função dada quando x tende para 0. Para isso, precisamos fazer o limite quando x é negativo e quando x é positivo. Então precisaremos fazer os limites laterais para o ponto 0. Primeiro o limite pela esquerda:
E Isso será:
Agora fazendo o limite pela direita:
Resultando em:
Como os dois resultados são iguais, o limite existe e é .
Passo 3
Para a letra (c), aplicaremos a definição de derivada sobre a nossa função com o limite primeiro tendendo a 0 pela esquerda e depois pela direita, para mostrarmos que a derivada existe,
Primeiro pela esquerda:
E agora pela direita:
Como os resultados são iguais, então existe e .
Resposta
Ei, a resposta está no passo a passo :)